Iako u prirodnim naukama preovlađuje induktivni metod, u njima ima i dedukcije, odnosno logičkog izvođenja posledica iz pretpostavki. Dedukcijom se povezuju principi i zakoni, pored toga, pomoću dedukcije predviđamo događaje koji će se dogoditi ako je neka hipoteza tačna. Jedino što dedukcijom ne radimo jeste proveravanje nekog prirodnog zakona – to uvek radimo pomoću eksperimenata, […]
Continue Reading
Metodologija društvenih nauka
Rekli smo da je karakteristika društvenih nauka to što se one bave razumevanjem čovekovog sveta, sveta koji on stvara kao slobodno biće. Iz ove glavne karakteristike društvenih nauka slede i ostale osobine metodologije društvenih nauka. Osnovna metoda koja je specifična za društvene nauke je razumevanje teksta, odnosno, znakova i jezika koji nam otkrivaju misli i […]
Continue Reading
Kriterijum nauke
Kada se posmatraju razna znanja, postavlja se pitanje po čemu se nauka razlikuje od onoga što nije nauka, odnosno po kom kriterijumu određujemo da jenešto nauka. Metodolozi su uvek želeli da otkriju ovaj kriterijum da bi jasnije omeđili i opisali način na koji nauka funkcioniše, čime bi bavljenje naukom postalo lakše i jednostavnije, između ostalog […]
Continue Reading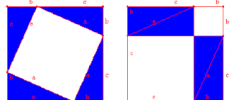
Deduktivni i induktivni dokaz
Dokazivanje se može definisati kao proces navođenja argumenata za neku tvrdnju. Kada nešto dokazujemo, navodimo jedan skup iskaza kao opravdanje za prihvatanje tvrdnje čiji nas dokaz interesuje. Da bismo taj odnos objasnili, poći ćemo od najjednostavnijih primera. Dokaz da smo bili u nekom gradu mogu biti naše fotografije iz tog grada, naš kredibilitet kada tvrdimo […]
Continue Reading
Dokazivanje u aksiomatskom sistemu (primer Euklidove geometrije)
Logika i matematika su egzaktne nauke specifične po tome što se u njima sve opšte tvrdnje u principu mogu deduktivno dokazati iz skupa početnih stavova, koji se nazivaju aksiome, i usvojenih logičkih pravila. Zbog ove osobine logike i matematike, one se mogu urediti kao aksiomatski sistemi. Aksiomatski sistem je sistem naučnih tvrdnji i dokaza za […]
Continue Reading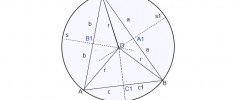
Direktni deduktivni dokaz
Kada nešto deduktivno dokazujemo, imamo dve mogućnosti: direktni deduktivni dokaz i indirektni deduktivni dokaz. Odnosno: 1) tezu možemo dokazivati direktno pokazujući da ona logički sledi iz aksioma sistema ili 2) možemo pokazati da antiteza (negacija teze) u sebi sadrži protivrečnost i da zbog toga nije tačna, što tezu čini tačnom, pa je ona dokazana indirektno. […]
Continue Reading
Indirektni deduktivni dokaz
U indirektnom deduktivnom dokazu tezu, odnosno, teoremu, dokazujemo tako što dokazujemo da negacija teze nije istinita. Ovaj isti postupak primenjivali smo kada smo metodom svođenja na protivrečnost dokazivali da je neka formula tautologija. Sada taj postupak možemo primeniti na bilo koju tezu. Da je negacija teze netačna dokazujemo tako što pokažemo da iz nje logički […]
Continue Reading
Matematička indukcija
Matematička indukcija je oblik deduktivnog zaključivanja (ime “indukcija” je dobila zato što samo liči na indukciju) koji se sastoji od dva koraka: najpre neku teoremu dokažemo za n=1, gde je n promenljiva koja može da uzme vrednost svih prirodnih brojeva (od 1 do ∞), i onda dokažemo da ako teorema važi za neku vrednost n, […]
Continue Reading
Induktivni dokaz
Već smo u početnoj lekciji ovog odeljka rekli da, osim deduktivnog dokaza, postoji i induktivno dokazivanje i induktivni dokaz. Rekli smo i da je samo prvi, deduktivni dokaz, dokaz u striktno logičkom smislu, odnosno, samo u deduktivnom dokazu važi da ako su argumenti istiniti, teza ili teorema mora biti istinita, što znači da je striktno […]
Continue Reading
Definicije, klasifikacije, iskazi, Logika
Pojam iskaza
Iskaz se u logici definiše kao rečenica koja može biti istinita ili lažna, odnosno, kao rečenica za koju ima smisla pitati da li je istinita ili lažna. Iskazi se po ovoj osobini razlikuju od mnogih drugih vrsta rečenica. Pitanja, molbe i naredbe, na primer, nisu iskazi jer se u odnosu na neko pitanje ili molbu […]
Continue Reading
Definicije, klasifikacije, iskazi, Logika
Vrste iskaza
Tautologije, kontradikcije i iskazi o stvarnosti Kao što smo već rekli, iskaze koji su logički istiniti zovemo “tautologije”, a iskaze koji su logički neistiniti “kontradikcije”. Tautologija je iskaz koji je uvek tačan, na primer: “Telo se kreće ili se ne kreće.” Kontradikcija je iskaz koji istovremeno tvrdi i neki stav i njegovu negaciju, na primer […]
Continue Reading
Definicije, klasifikacije, iskazi, Logika
Odnosi iskaza u tradicionalnom LOGIČKOM KVADRATU
Najpre ćemo ponoviti kako se iskazi koji imaju predikatsku formu (S ni/je P) dele po kvantitetu i kvalitetu. Po kvantitetu iskazi se dele na univerzalne, partikularne i singularne. Univerzalni iskazi govore nešto o svim članovima neke klase, partikularni tvrde da barem jedan član klase ima neku osobinu (a možda i svi), a singularni govore o […]
Continue Reading
Definicije, klasifikacije, iskazi, Logika
Odnosi iskaza u logičkom kvadratu po savremenom tumačenju
Za razliku od tradicionalnog tumačenja odnosa iskaza u logičkom kvadratu, u savremenom tumačenju univerzalni iskazi „Svi S su P“ i „Nijedan S nije P“ tumače se kao hipotetički iskazi, dok su partikularni iskazi zadržali egzistencijalno značenje. To znači da se „Svi S su P“ sada tumači kao „Za svako x važi da ako je x […]
Continue Reading
Zaključivanje
Zaključivanje je možda najbolje definisao Imanuel Kant (Immanuel Kant, 1724-1804): zaključivanje je proces izvođenja jednog stava iz jednog ili više drugih stavova. Onda kada možemo opravdati uverenje da je zaključak već bio sadržan u premisama, odnosno, da zaključak mora biti istinit ako su premise istinite, onda je zaključivanje deduktivno. Ali, mi ne možemo da zaključujemo […]
Continue ReadingVideo - IQ2 - Slavoj Žižek
© 2025 Kratka istorija filozofije. Powered by WordPress.







