Već smo u početnoj lekciji ovog odeljka rekli da, osim deduktivnog dokaza, postoji i induktivno dokazivanje i induktivni dokaz.

Rekli smo i da je samo prvi, deduktivni dokaz, dokaz u striktno logičkom smislu, odnosno, samo u deduktivnom dokazu važi da ako su argumenti istiniti, teza ili teorema mora biti istinita, što znači da je striktno dokazana.

Svi ostali dokazi su samo induktivni. Kada za neku tezu navodimo argumente koji tu tezu dokazuju induktivno, onda mi prihvatamo tezu na osnovu tih argumenata ili dokaza, ali se uvek može pokazati da je teza u nekom slučaju netačna.

Na ovaj način funkcionišu sve prirodne nauke, fizika, hemija, biologija itd, i u tome je razlika ovih nauka i tzv. egzaktnih nauka kakve su logika i matematika.

U prvoj lekciji ovog odeljka već smo govorili o ključanju vode i pokazali da je moguće da voda ne ključa na 100 stepeni, na nekoj višoj nadmorskoj visini. Sada možemo da se prisetimo Paskalovog zakona. Paskalov zakon kaže: Pritisak na fluid koji miruje prenosi se podjednako na sve zidove suda, nezavisno od njihovog oblika. Postavlja se pitanje kako je Paskal mogao da proveri da li ovaj zakon važi, a odgovor je isti za sve prirodne nauke – mogao je da to učini samo eksperimentom. Međutim, pošto u formulaciji Paskalovog zakona imamo reč “sve” u delu “sve zidove suda” ovaj zakon ne može da se zaista proveri za svaku tačku. To znači da smo do uverenja o njegovom važenju došli na osnovu konačnog broja merenja pritiska u nekom fluidu i da je uvek moguće da pronađemo tačku koja bi ga opovrgla. Ta mogućnost ne mora da nas omete u korišćenju hidraulične prese, koja radi na osnovu Paskalovog zakona, ali nas uvek može držati otvorenim za nove eksperimente.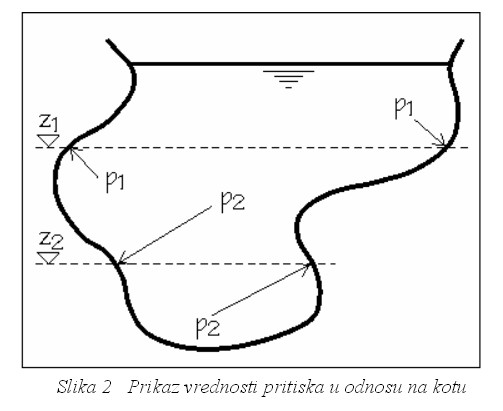

Razlog zašto u prirodnim naukama ne važe obavezno logički striktne veze oblika ako.. onda.. leži u tome što priroda, da tako kažemo, nema obavezu da uvek sledi naše potrebe pojednostavljenja i da bude uniformna. U stvari, priroda se javlja u mnogo varijacija i te varijacije ne možemo logički predvideti.

Svet gljiva (pečuraka) je dobra ilustracija za ovu osobinu prirode. Na zemlji ima oko 30.000 vrsta do sada pronađenih gljiva. Izgleda da se priroda nije potrudila da na logički striktan način poveže spoljni izgled gljiva i njihovu otrovnost za čoveka, tako da ne možemo utvrditi jasan kriterijum, prema spoljnjem izgledu, koja je gljiva otrovna. Ponekad se uzima da je taj kriterijum jarka boja ili prsten oko stabla gljive, ali ni to nije uvek znak otrovnosti.

Međutim, zamislimo da se slučajno desilo da nije tako i da su biolozi otkrili 200 vrsta gljiva i da se opet desilo tako da su samo gljive jarkih boja otrovne, a one blažih nijansi jestive. Šta bi neki biolog koji otkrije 201 vrstu, koja recimo nema jarku boju, trebalo da zaključi o njenoj otrovnosti? Čak i najbolji biolog ( i upravo on), znao bi da unapred ne može da zaključi ništa. To što je 100 gljiva blage boje bilo jestivo, ne znači da takva mora biti i 101 takva gljiva, što pokazuje da poznavanje strukture nauke može biti i životno važno. Ovo neznanje nije posledica toga što neko nije dobar biolog, već je to posledica vrste znanja koje se pojavljuje u prirodnim naukama. U toj vrsti znanja ne možemo da utvrdimo sigurne (logički dokazane) veze između raznih karakteristika predmeta.

Osobina prirode da nije uvek uniformna, ponekad se ispostavlja kao veoma korisna za nas. Na primer, zahvaljujući tzv. anomaliji vode omogućene su važne karakteristike prirode. Iako u principu u celoj prirodi važi da se tela sa povećanjem njihove toplote šire, a sa smanjenjem toplote skupljaju, odnosno postaju gušća, to ne važi za vodu koja je najgušća na temperaturi +4 Co. Zbog ove osobine vode led koji je lakši od vode pluta na vodi, što omogućava sadašnji eko-sistem. Gornji sloj leda štiti ostalu vodu od zaleđivanja pa zbog toga živi svet može da prezimi u njoj, što ne bi bilo moguće da je led teži od vode. Širenje vode pri prelasku u led dovelo je i od drobljenja stena i stvaranja plodnog tla za vegetaciju. Dakle, da nema vode i njene anomalije pitanje je da li bi živi svet kakav poznajemo bio moguć.

Induktivno dokazivanje nije sigurno ni u matematici u kojoj se i inače primenjuje samo kao pomoćna metoda. Na primer, iako su 7, 17, 37, 47, 67, 97, 107, prosti brojevi, odatle ne bi trebalo zaključiti da su svi brojevi koji se završavaju cifrom 7 prosti, pošto 27, 57, 77, 87, 117 nisu takvi.

Pitanjima strukture raznih nauka i metodama koje su primerene raznim naukama bavi se metodologija.

Ključne reči: induktivni dokaz, prirodne nauke, egzaktne nauke, Paskalov zakon, anomalija vode, metodologija

Rezime: Kada nešto dokazujemo u prirodnim i društvenim naukama to radimo navodeći primere iz iskustva koji potvrđuju tezu koju branimo. Ove primere možemo pronaći sistematskim istraživanjem, posmatranjem, eksperimetisanjem. Međutim, na ovaj način se nikada do kraja ne može dokazati neka teza izražena u obliku univerzalnog suda (koji se odnosi na više slučajeva od onih koje smo mogli da ispitamo). Kao ilustracija, u lekciji se pominju primeri Paskalovog zakona, carstva gljiva i tzv. “anomalija vode”.

Vežbanje:

Kao primer induktivnog dokazivanja teze navešćemo primere iz eksperimentalne psihologije, tačnije eksperimentalne socijalne psihologije. Teza je da ljudi, ako znaju da neka grupa ljudi ima jednu zajedničku osobinu, imaju tendenciju da misle da su im zajedničke i druge osobine, osim ove. Da bi se to eksperimentalno dokazalo, psiholozi su smislili ovakav eksperiment.

Stvaranje stereoptipa

Ispitanicima je pokazano osam linija dužine od 20 do 35 cm. Linije su pokazivane u grupi od manjih ka većim linijama i ispitanici su zamoljeni da procene odnos između četvrte i pete linije (koje su bile iste). To su radili na dva načina. Najpre su linije pokazane bez drugih oznaka, a zatim kao podeljene u dve grupe, grupu A u kojoj su bile kraće linije i četvrta među njima, i grupu B u kojoj su duže linije sa petom na početku (i dalje su linije bile poređane po veličini, samo su sada podeljene u dve grupe).

Ponovite u razredu ovaj eksperiment i pokušajte da izvedete zaključak. Da li je dužina četvrte i pete linije isto ocenjena u oba slučaja?

Grupni konformizam

U drugom eksperimentu, psiholozi su dokazivali tezu da su ljudi skloni da se priklanjaju mišljenju većine, čak i kada im sopstveni razum govori drugačije. Ispitanicima su pokazane linije na slici i pitani su koja od tri linije na desnoj strani je ista kao linija na levoj strani. Ukoliko su svi članovi grupe govorili da je je to neka od linija (po instrukcijama dobijenim od voditelja eksperimenta) član grupe koji nije bio instruiran se u značajnom procentu slagao sa grupom, iako mu je vlastiti razum govorio da je odgovor drugih članova grupe netačan.

Antrfile:

Dejvid Hjum (David Hume, 1711 – 1776) bio je filozof iz 18.veka koji je živeo u Edinburgu u Škotskoj. Hjum je do krajnosti doveo stanovište da sve saznajemo iz iskustva. Problem koji mu se ukazao kada je pretpostavio da sve saznajemo pomoću iskustva, bio je da u tom slučaju nijednu iskustvenu činjenicu ne možemo logički da izvedemo iz druge. Na primer, uvek je moguće da se nešto dešavalo u prošlosti, a da se neće na isti način dešavati u budućnosti. Ili, uvek je moguće da u jednom kraju sveta ili kosmosa važi jedno pravilo a u drugom drugo. Hjum je na ovaj način objasnio i naglasio logičku prirodu induktivnog dokaza o kome smo govorili u lekciji. Induktivni dokaz daje samo hipotetička ili verovatna znanja. U prirodnim naukama nije moguća apsolutna izvesnost.