Kada nešto deduktivno dokazujemo, imamo dve mogućnosti: direktni deduktivni dokaz i indirektni deduktivni dokaz. Odnosno:
1) tezu možemo dokazivati direktno pokazujući da ona logički sledi iz aksioma sistema ili
2) možemo pokazati da antiteza (negacija teze) u sebi sadrži protivrečnost i da zbog toga nije tačna, što tezu čini tačnom, pa je ona dokazana indirektno.
U ovoj lekciji obradićemo samo prvi način: direktni deduktivni dokaz.
Da bi nešto mogli direktno deduktivno dokazati, potreban nam je aksiomatski sistem o kome smo govorili u prošloj lekciji. Tada su nam na raspolaganju aksiome, ranije dokazane teoreme i logička pravila pomoću kojih možemo svoju teoremu izvesti iz ovih aksioma i ranije dokazanih teorema (pomoćnih teorema).
Kao što smo već rekli, prvi aksiomatski sistem bila je geometrija. U dokazima u geometriji možemo pratiti kako se na osnovu jednostavnih uvida može doći do zaključaka koji uopšte nisu očigledni.na prvi pogled.
Poći ćemo od dokaza jedne jednostavne geometrijske teoreme:
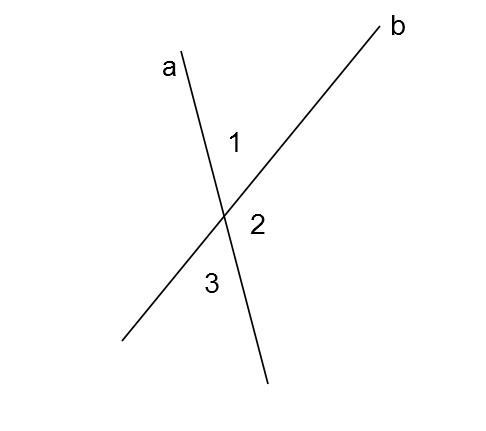
U slučaju dve prave koje se seku, naspramni uglovi su jednaki. Na slici, uglovi 1 i 3 su jednaki, kao i 2 i njemu naspramni ugao. (koristimo brojeve za oznaku uglava iz tehničkih razloga)
Ova se teorema može dokazati pozivanjem na jednu pomoćnu teoremu: Svi uglovi nad jednom pravom su jednaki (iznose 180 stepeni) i na logičko pravilo, koja navodi i Euklid: kada se od jednakih veličina oduzme jednaka veličina, ostaci su jednaki.
U našem slučaju: ugao 1 + ugao 2 = 180 i ugao 2 + ugao 3 = 180, odnosno, < 1 = 180 – < 2 i < 3 = 180 – < 2, odakle sledi – opet po logičkom pravilu da ako su dve veličine jednake nekoj trećoj veličini jedanke su i međusobno – da je < 2 = < 3, što smo i hteli da dokažemo.
Ako sada krenemo dalje, možemo dokazati i novu teoremu:
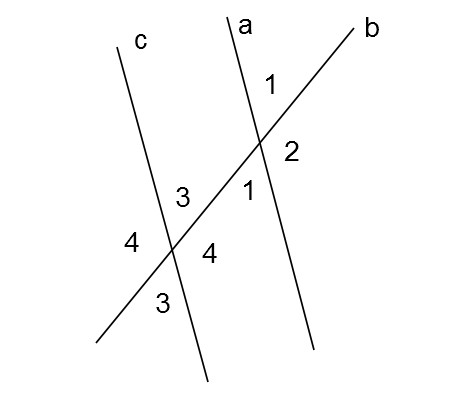
Analogni naspramni uglovi koji nastaju kada jedna prava seče dve paralelne prave takođe su jednaki. Odnosno, na gornjoj slici, uglovi 1 i 3 jednaki su.
Pomoćna teorema za ovaj dokaz je stav da je zbir uglova < 1 + < 4 = 180 (ovo neposredno sledi iz 5. aksiome Euklidove geometrije) a takođe i da je < 4 + < 3 = 180 (pošto su to dva ugla nad jednom pravom) . Po istoj logici kao malopre, onda je < 3 = 180 – < 4, a < 1 = 180 – < 4, što znači da su < 1 i < 3 jednaki.
Ove teoreme čine nam se i intuitivno očigledne. Pa ipak, samo na osnovu njih možemo dokazati da je zbir uglova u trouglu uvek jednak 1800 , što je već manje očigledno na prvi pogled.
Kako bi došli do potrebnih jednakih uglova, najpre je potrebno da produžimo jednu stranicu trougla (a) i da povučemo pravu koja je paralelna stranici c, a prolazi kroz naspramno teme trougla (kao na slici). Prethodno dokazana teorema o jednakosti analognih naspramnih uglova biće nam pomoćna teorema u ovom dokazu. Po toj teoremi uglovi 1 i 1 (u plavoj boji) su jednaki, a takođe i uglovi 3 i 3 (u plavoj boji), a pošto je < 2 + < 3 + < 1 = 180 (uglovi nad pravom) onda je i < 2 + < 3 + 1 = 180, što je i trebalo dokazati.
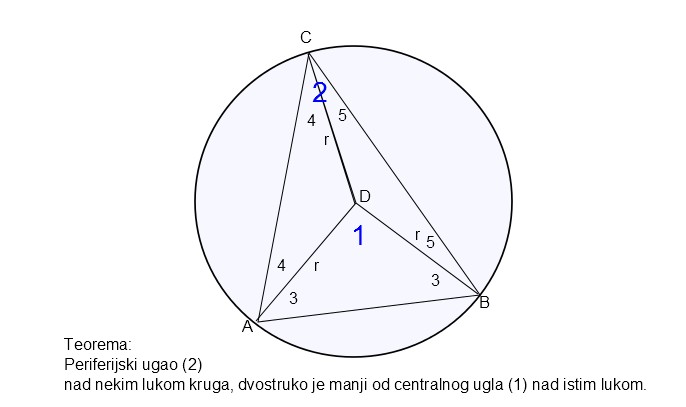
Kada ovo znamo, možemo da idemo dalje. Na primer, možemo dokazati teoremu da je periferijski ugao nad jednim kružnim lukom dvostruko veći od centralnog ugla nad istim kružnim lukom. Odnosno:
Prva pomoćna teorema nam je stav da pošto su trouglovi ADC, CDB i ADB jednakokraki (ti krakovi su poluprečnici kruga koji su svi po definiciji jednaki), onda su po dva ugla u tim trouglovima jednaki. Na slici, oni su označeni brojevima 4 i 4, 5, i 5, 3 i 3.
Osim toga, treba nam i druga pomoćna teorema da je zbir uglova u trouglu uvek 180.
Ako sada posmatramo dva trougla ABC i ABD koji sadrže uglove koji nas zanimaju, uglove < 1 i < 2, onda znamo da je i njihov zbir uglova 1800.
Odnosno:
< 4 + < 4 + < 5 + < 5 + < 3 + < 3 = 180 i
< 3 + < 3 + < 1 = 180
Ako spojimo ove dve jednačine, dobijamo < 4 + < 4 + < 5 + < 5 + < 3 + < 3 = < 3 + < 3 + < 1, i ako skratimo < 3 + < 3 na obe strane, dobijamo da je dvostruko < 4 + < 5 jednako uglu < 1, a pošto je zbir uglova < 4 i < 5 jednak uglu koji smo označili brojem < 2, onda je 1 jednako dvostrukom < 2, što je i trebalo dokazati.
Na ovaj način, dokazali smo i više: da su svi periferijski uglovi nad nekim kružnim lukom jednaki, što je daleko od očiglednog na prvi pogled.
Dakle, postupno dokazivanje u geometriji može nam deduktivno, tj. sasvim sigurno, dokazati mnoge stvari koje inače ne bismo znali.
Dokazaćemo još jednu teoremu:
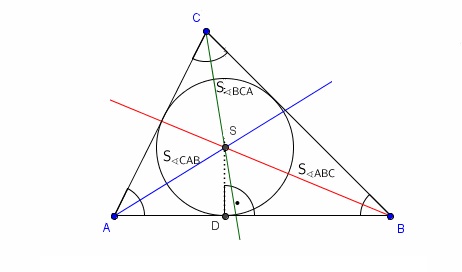
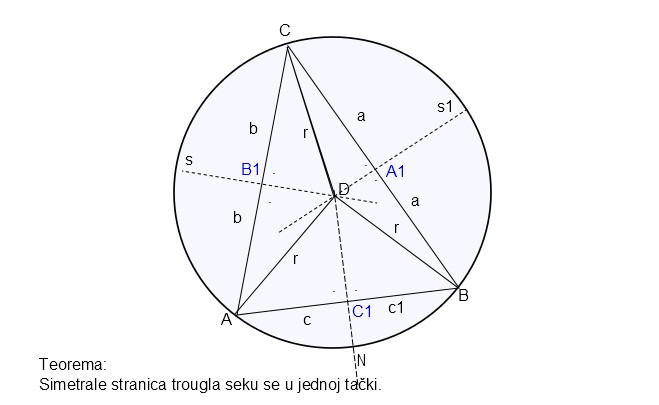
Teorema: Simetrale stranica trougla seku se u jednoj tački koja je istovremeno centar opisanog kruga nad trouglom.

Dokazivanje počinjemo tako što povučemo dve simetrale i iz tačke u kojoj se one seku spustimo normalu na treću stranicu. Ako dokažemo da je ta normala simetrala, što će biti dokazano ako stranicu seče na dva jednaka dela (c i c1 na slici), onda smo dokazali našu teoremu.
Pomoćne teroeme i logička pravila koja su nam potrebna:
1) Trouglovi koji imaju jednake dve stranice i uglove između njih, jednaki su međusobno.
2) Trouglovi koji imaju jednake dve stranice i uglove naspram veće od njih, jednaki su međusobno.
a) Ako su dve duži jednake sa nekom trećeom duži, jednake su međusobno.
Na osnovu ovih teorema (i pravila), možemo da utvrdimo da su mali trouglovi koji nastaju nad stranicom AC jednaki (ADB1 i CDB1), pa je zbog toga AD=CD, a isto važi i za male trouglove koji nastaju oko simetrale S1 – CDA1 i DBA1 odakle sledi da je CD=DB, pa su po logičkom pravilu a i AD=DB, a onda su po drugoj pomoćnoj teoremi i trouglovi ADC1 i BDC1 jednaki, što znači da je c=c1, odakle sledi da je normala N simetrala nad trećom stranicom, a to smo i hteli da dokažemo. Pošto se na ovaj način sve simetrale trougla seku u jednoj tački, a pošto je i AD=CD=BD, onda se iz tačke D može opisati krug oko trougla.
Većina dokaza u matematici su direktni dokazi, međutim, ponekad je neku teoremu teško dokazati direktno.
Zbog toga postoji indirektni deduktivni dokaz (dokaz svođenjem na apsurd).
Vežba:
pokušaj dokazati sledeće geometrijske teoreme.
1) Talesova teorema: Periferijski ugao nad prečnikom kruga uvek iznosi 90 stepeni.
2) Simetrale uglova trougla seku se u jednoj tački.
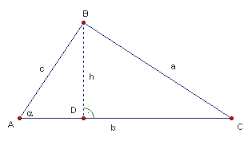
3) Površina trougla jednaka je polovini proizvoda dužine jedne stranice i dužine visine trougla u odnosu na tu stranicu.
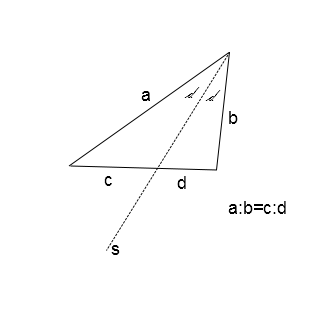
4) Simetrala ugla trougla seče naspramnu stranicu u srazmeri stranica trougla koje čine ugao na kome je simetrala.
dodatak:
Zanimljiv dokaz da se visine trougla seku u jednoj tački (koja se inače zove Ortocentar, a obeležava sa H) koji se oslanja na ovde prikazani dokaz da se simetrale stranica seku jednoj tački, možete pronaći ovde.
Dokaz da se težišne linije seku u jednoj tački poziva se na sinusnu teoremu.