Logika i matematika su egzaktne nauke specifične po tome što se u njima sve opšte tvrdnje u principu mogu deduktivno dokazati iz skupa početnih stavova, koji se nazivaju aksiome, i usvojenih logičkih pravila.

Zbog ove osobine logike i matematike, one se mogu urediti kao aksiomatski sistemi.

Aksiomatski sistem je sistem naučnih tvrdnji i dokaza za te tvrdnje koji ima tri dela:
1) Aksiome (tvrdnje koje se u okviru sistema ne dokazuju, ali se sve druge tvrdnje dokazuju na osnovu njih)
2) Teoreme (tvrdnje koje se dokazuju na osnovu aksioma)
3) Logička pravila pomoću kojih povezujemo aksiome i teoreme.

Prvi aksiomatski sistem sastavio je Euklid u 3. veku p.n.e. U njemu je geometrija predstavljena kao aksiomatski sistem koji ima svoje definicije, aksiome, teoreme i pravila dokazivanja. Na primer, tačka je definisana kao “ono što nema delova”, linija kao “dužina bez širine”, krug kao geometrijsko mesto tačaka koje su na istom odstojanju od jedne tačke itd.

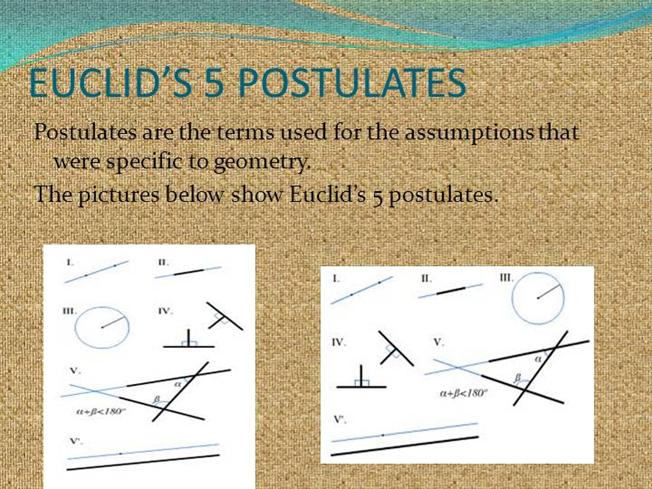
Geometrijske aksiome (kod Euklida se koristi termin “postulati”) formulisane su ovako:
“Neka se pretpostavi

1. Da se može povući od svake tačke ka svakoj drugoj tački prava linija.

2. I da ograničena prava može biti produžena u svom pravcu neprekidno.

3. I da se može opisati iz svakog središta svakim rastojanjem krug.

4. I da su svi pravi uglovi jednaki međusobno.

5. I da će se, ako jedna prava u preseku sa drugim dvema obrazuje sa iste strane dva unutrašnja ugla čiji je zbir manji od dva prava ugla, te dve prave, beskrajno produžene, seći i to sa one strane sa koje su ovi uglovi manji od dva prava.”
A pravila su tipična logička pravila, ovog tipa:

“1. Oni (objekti) koji su jednaki istom (objektu) jednaki su međusobno.

2. I ako se jednakim (objektima) dodaju jednaki (objekti) celine su jednake” itd.

(na linku http://poincare.matf.bg.ac.rs/nastavno/zlucic/ možete pronaći kompletan spisak Euklidovih definicija, postulata i aksioma)

Na osnovu ovih aksioma i pravila Euklid je dokazao 463 teoreme koje su sačinjavale tadašnju geometriju.

Logika i matematika su jedine discipline koje se mogu izgraditi kao aksiomatski sistemi, pa su to i jedine discipline u kojima postoji ustanovljeni precizan način za dokazivanje tvrdnji. Jedino u njima su na striktno deduktivan način dokazane teoreme kroz jedan uređen sistem koji se sastoji od poznatog konačnog skupa aksioma, istog takvog skupa pravila i obimnog skupa teorema koje ispunjavaju gotovo čitavu oblast istraživanja, kakva je, na primer, geometrija.

Ova osobina logike i matematike uvek je intrigirala naučnike i filozofe koji su bili fascinirani mogućnošću da se matematički stavovi deduktivno dokažu.