Najpre ćemo ponoviti kako se iskazi koji imaju predikatsku formu (S ni/je P) dele po kvantitetu i kvalitetu.

Po kvantitetu iskazi se dele na univerzalne, partikularne i singularne. Univerzalni iskazi govore nešto o svim članovima neke klase, partikularni tvrde da barem jedan član klase ima neku osobinu (a možda i svi), a singularni govore o jednom pojedinačnom članu klase.

Po kvalitetu iskazi se dele na afirmativne, negativne i limitativne. Afirmativni tvrde da subjekt ima neku osobinu, negativni da nema neku osobinu, a limitativni da ima neku osobinu koja je opisana negacijom.

U tabeli to izgleda ovako:

Dakle, univerzalni stavovi mogu biti i afirmativni i negativni i limitativni, kao i partikularni i singularni stavovi. Ali u logičkom kvadratu javljaju se samo univerzalni i partikularni, odnosno afirmativni i negativni stavovi, u svim kombinacijama.

Primere logičkih kvadrata možemo napraviti polazeći od univerzalno-afirmativnih stavova:

Svi dobri filmovi su holivudski.

Svi fakulteti su privatni.

Svi ljudi su dobri.

Svaki realiti-šou je dosadan.

Svi beogradski tramvaji su udobni.

Kakvi odnosi postoje u logičkom kvadratu? Prvo ćemo obraditi tradicionalno  tumačenje logičkog kvadrata, a onda i savremeno tumačenje.

Tradicionalno tumačenje odnosa u logičkom kvadratu

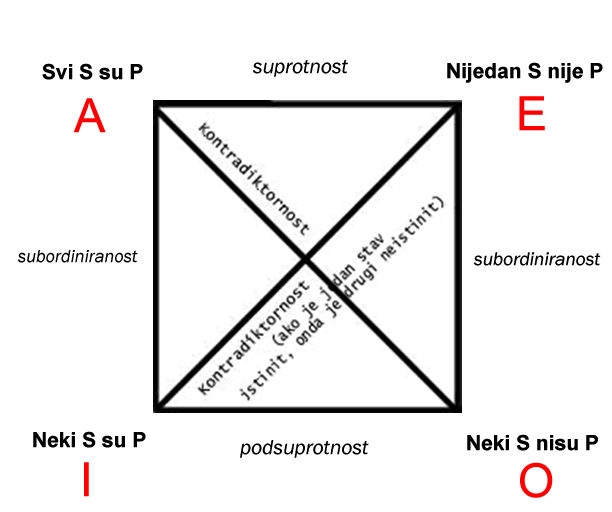
Da počnemo od kontradiktornosti.

Stavovi koje spajaju dijagonale kvadrata su kontradiktorni, što znači da ako je stav na jednom kraju dijagonale istinit, stav na drugom mora biti neistinit, i obrnuto, ako je stav na jednom kraju neistinit, satv na drugom je istinit.

na primer, Ako je tačno  da su svi ljudi dobri, onda nije tačno da neki ljudi nisu dobri.

Stavovi “Svi ljudi su dobri” i “Nijedan čovek nije dobar” su kontrarni (suprotni). To znači da ako je jedan od tih stavova istinit, drugi mora biti neistinit. Ali, ako je jedan od tih staviova neistinit, drugi ne mora biti istinit. Drugim rečima, kontrarni stavovi mogu oba biti neistiniti, kao što boja nečega može biti i drugačija, a ne samo bela ili crna.

Stavovi “Svi ljudi su dobri” i “Neki ljudi su dobri” su subordinirani. To znači da ako je stav “Svi ljudi su dobri” istinit, stav “Neki ljudi su dobri” mora biti istinit. Obrnuto ne važi – ako je stav “Neki ljudi su dobri” istinit, stav “Svi judi su dobri” ne mora biti istinit.

Međutim, ako stav “Svi ljudi su dobri” nije istinit, ne mora biti istinit ni stav “Neki ljudi su dobri”. Isto važi i za subordiniranost na negativnoj strani.

Stavovi “Neki ljudi su dobri” i “Neki ljudi nisu dobri” su podsuprotni ili subkontrarni. To znači da oni mogu biti oba istiniti, kao kada kažemo “Neki jesu, a neki nisu…”, ali ne mogu biti oba neistiniti, jer mora biti da je tačno da članovi klase jesu ili nisu nešto, ovde mora biti tačno da su članovi klase ili dobri ili nisu dobri. Takođe, jedan iskaz iz para podsuprotnih iskaza može biti istinit, a jedan nesitinit, pošto je značenje iskaza “Neki S su P” – “Neki S, a možda i svi su P”, a u slučaju da su svi S P, nije tačno da neki S nisu P.

Da bi se lakše snalazili u logičkom kvadratu još u srednjem veku svakom stavu u logičkom kvadratu pridruženo je jedno veliko slovo.

univerzalno-afirmativnom sudu    A

univerzalno-negativnom    E

partikularno-afirmativnom      I

partikularno-negativnom      O

dakle, A E I O.

Savremeno tumačenje odnosa u logičkom kvadratu

U savremenom tumačenju logičkog kvadrata univerzalni sudovi se tumače tako da ne tvrde egzistenciju, nego samo hipotetičku vezu, dok partikularni sudovi tvrde egzistenciju.

To znači da se iskaz:

“Svi ljudi su dobri”tumači kao “ako postoji nešto takvo kao čovek, onda su svi ljudi dobri”

međutim, iskaz “Neki ljudi su dobri” tumači se kao “Postoji barem jedan čovek koji je dobar”.

To znači da se u savremenom tumačenju menjaju neki odnosi među ovim stavovima. O tome u sledećoj lekciji.

Ključne reči: logički kvadrat, A – univerzalno-afirmativan stav, E – univerzalno-negativan stav, I – partikularno-afirmativan stav, O – partikularno-negativni stav, kontradiktornost, protivrečnost, kontrarnost, suprotnost, subkontrarnost, podsuprotnost, subordiniranost/superordiniranost, podređenost/nadređenost.

Rezime: Logički kvadrat je uređen način da se analiziraju odnosi između 4 oblika iskaza izrečenih u predikatskoj formi (S je/nije P). Ta četiri oblika iskaza su: univerzalno-afirmativan iskaz, univerzalno-negativan iskaz, partikularno-afirmativan iskaz i partikularno-negativni iskaz. Ovi se iskazi tradicionalno obeležavaju slovima, redom: AEIO. Između ovih iskaza, protumačenih na tradicionalan način (kao da ono o čemu iskazi govore nedvosmisleno postoji), postoje 4 vrste odnosa: protivrečenost, suprotnost, podređenost/nadređenost i podsurotnost.

Vežbanja:

1) Na nekoliko primera logičkih kvadrata provežbajte svoje znanje o odnosima u tradicionalnom logičkom kvadratu. Možete poći od ovih univerzalno-afirmativnih stavova a onda izmisliti i svoje:

Svi naučnici su bogati.

Sva jedra su bela.

Sve ruže mirišu.

• Popunite donju šemu znacima za tačan iskaz (T), netačan (┴) i znakom da se istinitosna vrednost ne može odrediti, odnosno, da može biti i tačna i netačna (T, ┴). Reper za zaključivanje je zadata vrednost na početku strelice.

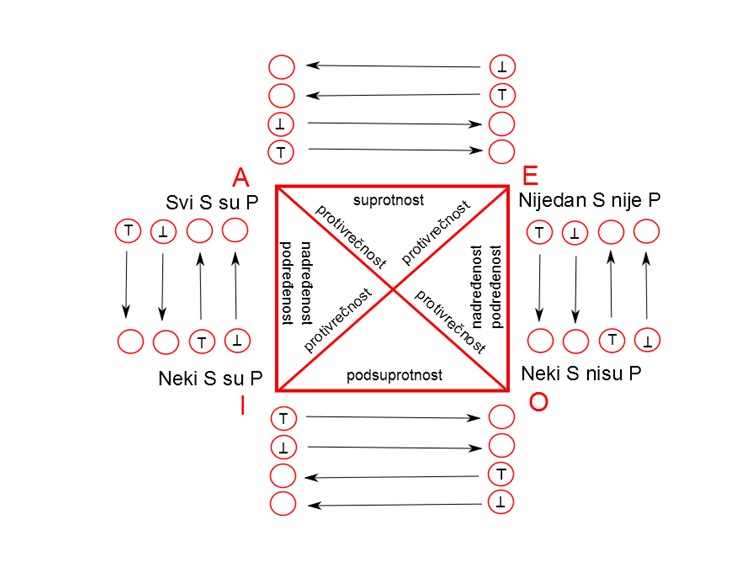
Docrtajte sami i dodatak ovoj šemi u kome bi bio prikazan i odnos protivrečnosti.