Tautologije, kontradikcije i iskazi o stvarnosti
Kao što smo već rekli, iskaze koji su logički istiniti zovemo “tautologije”, a iskaze koji su logički neistiniti “kontradikcije”. Tautologija je iskaz koji je uvek tačan, na primer: “Telo se kreće ili se ne kreće.” Kontradikcija je iskaz koji istovremeno tvrdi i neki stav i njegovu negaciju, na primer “Danas je sunčano i nije sunčano”. Kontradikcija je iskaz koji je uvek netačan, nezavisno od toga kakav je svet, u našem slučaju, kakvo je danas vreme.
Kontradikcije i tautologije u svetu iskaza predstavljaju dve krajnosti (suprotnosti) koje na neki način oivičavaju svet. Između njih postoji mnoštvo iskaza koji nisu ni logički istiniti ni logički lažni, već su istiniti ili lažni u zavisnosti od toga kakav je svet ili stvarnost zaista. A kakav je svet zaista nekada znamo sa većom pouzdanošću, a nekada sa manjom, tako da nam nije uvek lako da odredimo da li je iskaz faktički istinit ili lažan.
Predikativni, relacioni i egzistencijalni iskazi
Prema opštem obliku iskaze možemo podeliti na predikativne, relacione i egzistencijalne iskaze.
Predikativni iskazi tvrde da se nekom subjektu može pripisati neki predikat ili neka osobina: “Platon je osnivač Akademije”. U ovom iskazu “Platon” je subjekat, “osnivač Akademije” je predikat, a povezuje ih veznik “je”. Aristotel je smatrao da se svi iskazi mogu prevesti na predikatvnu formu, ali danas razlikujemo još najmanje dve forme iskaza: relacionu i egzistencijalnu.
Relacioni iskazi tvrde da su dva ili više predmeta (u najširem smislu termina) u nekoj relaciji – “Jelena i Ana su sestre” ili “5 je veće od 3”, “Tačke A, B, C nalaze se u istoj ravni” “Jovan Jovanović Zmaj i Nikola Tesla su savremenici” itd.
Egzistencijalni iskazi tvrde na nešto postoji ili ne postoji, na primer “Postoji najveći prost broj” ili “Okrugli kvadrati ne postoje” ili “Slatkovodni delfini postoje”.
Predikativni iskazi su u modernoj logici protumačeni kao relacioni iskazi. Tako je na primer “Svi galebovi su beli” postalo “Za svako x, ako je x galeb, onda je x belo”. Forma ovog drugog iskaza kaže da jedna osobina “biti galeb” implicira osobinu “biti beo”, odbosno, da su te dve osobine u logičkoj relaciji impliciranja.
Kvalitet i kvantitet iskaza
Predikativni iskazi se u klasičnoj logici dele prema kvalitetu i kvantitetu.
Prema kvalitetu dele se na afirmativne i negativne iskaze. Afirmativni iskazi tvrde da nešto jeste, odnosno da nešto ima neku osobinu: “Svi fudbaleri Barselone su brzi”, a negativni iskazi tvrde da nešto nije, odnosno, da nešto nema neku osobinu: “Neki fudbaleri Barselone nisu spori”.
Prema kvantitetu iskazi se mogu podeliti na univerzalne, partikularne i singularne iskaze. Univerzalni iskazi tvrde nešto o svakom članu neke klase objekata: “Svi elektroni imaju spin”. Partikularni sudovi tvrde da neki, a možda i svi (dakle “bar neki”, odnosno, “bar jedan”) članovi neke klase imaju (ili nemaju) neku osobinu: “Neke stonoteniserke su iz Kine”. Singularni sudovi tvrde nešto o jednom pojediničnom predmetu: “Kladovo je grad na obali Dunava”. Singularni stavovi se mogu protumačiti kao specijalni slučaj univerzalnih stavova koji govori o svim članovima nekog skupa, s tim da taj skup ima samo jedan član.
Kvalitet i kvantitet imaju svi predikativni iskazi pa su moguće različite kombinacije ovih osobina.
Kategorički i hipotetički iskazi
Kategorički iskazi su iskazi kojima se naprosto nešto tvrdi, kao što smo malopre predikativnim iskazima tvrdili da nešto ima neku osobinu. Hipotetički iskazi tvrde da će se nešto dogoditi ili da se nešto može tvrditi pod nekim uslovom, pa imaju formu “ako…..onda….” Recimo: “Ako u atmosferi neke planete ima puno kiseonika, onda na toj planeti ima života”.
Vrednosni i saznajni iskazi
Iskazi se mogu podeliti i na vrednosne i saznajne iskaze. Vrednosni iskazi operišu predikatom “dobro” i njegovim derivatima “ispravno”, “pravedno” “valjano”, “vredno” i odnose se na radnje koje možemo, ali ne moramo da preduzmemo. Saznajni iskazi, u užem smislu, opisuju stvarnost koja je nezavisna od naše volje, na primer “Mars je četvrta planeta od sunca”, “Ćelije biljke koriste vodu” itd.
Prosti i složeni iskazi
Sve iskaze takođe možemo podeliti na proste i složene. Složene iskaze možemo razložiti na više iskaza, a proste ne možemo. Složeni iskazi mogu se formirati od više prostih iskaza koji su povezani logičkim relacijama. Osnovnim logičkim relacijama, odnosno, logičkim operacijama pomoću kojih se od prostih iskaza mogu načiniti složeni iskazi, bavićemo se kasnije.
Ključne reči: vrste iskaza, tautologije, kontradikcije, afirmativni, negativni, univerzalni, partikularni, singularni, predikativni, relacioni, egzistencijalni, kategorički, hipotetički, vrednosni, saznajni, prosti i složeni iskazi.
Rezime: Iskazi se mogu podeliti na vrste po raznim kriterijumima. Najpre se iskazi mogu podeliti na predikativne, relacione i egzistencijalne. Klasična logika analizira samo predikativne iskaze i deli ih: 1) prema kvalitetu, na afirmativne i negativne, a 2) prema kvantitetu, na univerzalne, partikularne i singularne. Prema tome da li nešto tvrde pod nekim ekspliciranim uslovom ili ne, iskazi se dele na kategoričke i hipotetičke. Prema stepenu složenosti dele se na proste i složene, a prema oblastima na koje se odnose na vrednosne i saznajne.
Vežbanje:
Označite početnim slovima naziva za vrstu iskaza, kojim vrstama iskaza pripadaju sledeći iskazi:
Iskaz afirm./neg. pred./rel./egz. kat./hip. vred./sazn. prosti/složeni
Pariz je najlepši grad u Evropi.
Postoje životinje koje mogu da budu dugo bez vode.
Površina Kanade veća je od površine Sjedinjenih Država.
Nisam to rekao.
Ako ne požurimo, zakasnićemo.
Antrfile:
Gotlob Frege (Friedrich Ludwig Gottlob Frege, 1848-1925) veoma je uticao na moderne poglede na logiku. Predložio je jasnu analizu značenja termina i iskaza. Razlika konotacija – denotacija koju smo koristili u analizi pojma potiče iz njegovih spisa. U analizi iskaza, Frege je uvideo da se iskazi mogu analizirati kao funkcija svojih delova, odnosno da istinitosna vrednost složenih iskaza zavisi od istinitosnih vrednosti prostih iskaza iz kojih se složeni iskazi sastoje. Takođe, Frege je uočio da se predikatski iskazi mogu analizirati kao vrsta relacionih iskaza. Tako je univerzalno-afirmativni stav “Svi S su P”, protumačio kao iskaz u kome su u logičku relaciju implikacije stavljeni iskazi da je nešto S i da je nešto P, pa se iskaz “Svi S su P” može protumačiti kao hipotetički iskaz “Ako je neko x S, onda je to x i P”. Na taj način je logika, umesto da se bavi samo osobinama objekata, mogla da bude proširena iskazima koji su opisivali najrazličitije moguće relacije među objektima, koje ranije nisu bile u njenom fokusu.
Antrfile:
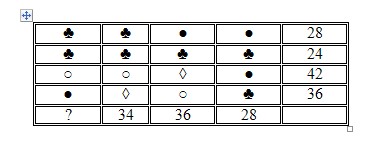
Mozgalica
Svaki od simbola u tabeli predstavla neki broj. Zbir svakog reda i zbir tri od četiri kolone dat je u tabeli. Odredite koja je vrednost svakog simbola. (zadatak 360 iz Male knjige velikih mozgalica).
