Metoda istinitosnih tablica je drugo ime za izračunavanje vrednosti složenih formula za sve kombinacije isitinitosnih vrednosti iskaznih promenljivih. Definicije logičkih operacija iz prošle lekcije su takođe male istinitosne tablice. Ako znamo ove tablice, koje definišu vrednosti složenih iskaza koji nastaju logičkim operacijama, možemo da izračunamo vrednost svake složene formule koja sadrži te operacije za svaku moguću vrednost iskaznih promenljivih.
Samo izračunavanje izgleda ovako:
|
p |
q |
p → (p ∙ q) |
Izračunata konjukcija u zagradi |
vrednost složene formule (izračunata implikacija) |
|
┬ |
┬ |
┬→ (┬∙┬) |
┬→ ┬ |
┬ |
|
┬ |
┴ |
┬→ (┬∙┴) |
┬→┴ |
┴ |
|
┴ |
┬ |
┴→ (┴∙┬) |
┴→┴ |
┬ |
|
┴ |
┴ |
┴→ (┴∙┴) |
┴→┴ |
┬ |
Dakle, kada koristimo metodu istinitosnih tablica, najpre napišemo sve kombinacije vrednosti iskaznih promenljivih (kombinacija uvek ima 2n, ako je n broj promenljivih), zatim, zamenimo te vrednosti u formuli i onda najpre izračunamo zagrade, a onda i celu formulu postupno.
Gornja formula je za jednu kombinaciju bila netačna, a za ostale kombinacije tačna.
Ako je formula tačna za sve kombinacije istinitosnih vrednosti iskaznih promenljivih ona je tautologija.
Ako nije tačna za sve kombinacije istinitosnih vrednosti iskaznih promenljivih ona je kontradikcija.
Ako je formula tačna bar za jednu kombinaciju istinitosnih vrednosti iskaznih promenljivih, formula je zadovoljiva.
Ako je formula nije tačna bar za jednu kombinaciju istinitosnih vrednosti iskaznih promenljivih ona je oboriva formula.
Iz ovih definicija sledi da su sve tautologije zadovoljive formule, ali da sve zadovoljive formule nisu tautologije, a sličan odnos je i kod kontradikcija: sve kontradikcije su oborive formule, ali sve oborive formule nisu kontradikcije. Jedna formula može istovremeno biti i zadovoljiva i oboriva.
Metoda istinitosnih tablica može se primeniti na svaku formulu. Ova formula je na priimer tautologija:
|
p |
q |
p → (p v q) |
Izračunata disjunkcija u zagradi |
vrednost složene formule (izračunata implikacija) |
|
┬ |
┬ |
┬→ (┬v┬) |
┬→ ┬ |
┬ |
|
┬ |
┴ |
┬→ (┬v┴) |
┬→┬ |
┬ |
|
┴ |
┬ |
┴→ (┴v┬) |
┴→┬ |
┬ |
|
┴ |
┴ |
┴→ (┴v ┴) |
┴→┴ |
┬ |
a ova kontradikcija:
|
p |
q |
(p → q) ∙ (p ∙ ¬q) (izračunata negacija q) |
Izračunate zagrade |
vrednost složene formule (izračunata implikacija) |
|
┬ |
┬ |
( ┬ → ┬) ∙ (┬∙┴) |
┬∙ ┴ |
┴ |
|
┬ |
┴ |
( ┬ → ┴) ∙ (┬∙┬) |
┴ ∙ ┬ |
┴ |
|
┴ |
┬ |
( ┴ → ┬) ∙ (┴∙┴) |
┬ ∙┴ |
┴ |
|
┴ |
┴ |
( ┴ → ┴) ∙ (┴∙┬) |
┬∙┴ |
┴ |
Na ovaj način možemo odrediti da li je neka formula tautologija ili kontradikcija ili ni jedno ni drugo.
Ključne reči: istinitosna tablica, tautologija, kontradikcija, zadovoljiva i oboriva formula
Rezime: Metodom istinitosnih tablica izračunavamo vrednost formule za sve moguće varijacije vrednosti iskaznih promenljivih. Pri tom koristimo definicije logičkih operacija. Na ovaj način možemo proveriti da li je neka formula tautologija (ukoliko dobijemo da je formula tačna za sve varijacije), kontradikcija (ukoliko je netačna za sve varijacije), zadovoljiva formula (ukoliko je tačna bar za jednu varijaciju) i oboriva formula (ukoliko je netačna bar za jednu varijaciju).
Vežbanje:
Izračunajte metodom istinitosnih tablica vrednosti sledećih formula:
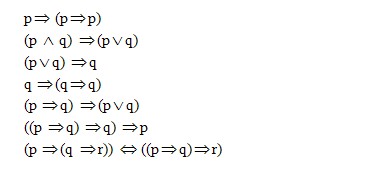
Antrfile: Programiranje i logika
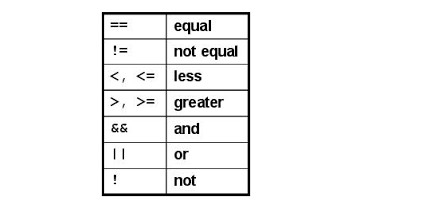
Već i letimičan pogled na programiranje pokazuje koliko je ono zasnovano na logici. Na primer, u iskaznom računu kojim se sada bavimo, postoje pravila za formiranje izraza iskaznog računa (sintaksa), a na isti način postoje pravila za pisanje programskog koda (sintaksa programskog jezika). Postoji i analogija između važne IF naredbe u programiranju i implikacije u iskaznom računu. IF naredba nam kaže šta treba da se dogodi ako je ispunjen određeni uslov “if (uslov) {izvršenje}”, a implikacija nam govori šta je tačno, ako je neki iskaz tačan “ako p, onda q”. U okviru programskog jezika C# postoje i znaci za logičke operacije: ! je znak za negaciju, && za konjunkciju, a || za disjunkciju. Takođe su tu i logičke konstante false (netačno) i true (tačno). Više o logičkim izrazima u programiranju možete naći na sajtu Matematičkog fakulteta u Beogradu: http://www.edusoft.matf.bg.ac.rs/csharp/Verzija2010/naredbe3.html
Operatori u programu C#