U prethodnoj lekciji upoznali smo se sa interpretacijom logičkih operacija (logičkih veznika) u svakodnevnom jeziku. Njihova precizna definicija data je preko istinitosnih tablica koje određuju kada je složeni iskaz koji nastaje logičkom operacijom istinit, a kada nije.

Istovremeno, ove tablice su neophodne za izračunavanje vrednosti složenih iskaza. Evo tih defincija:

Negacija (znak ¬ ) je ona logička operacija koja primenjena na neki iskaz daje iskaz suprotne istinitosne vrednosti. Dakle, kad je iskaz istinit, njegova negacija je neistinita i obrnuto. U tablici, to izleda ovako:

Konjukcija (znak ∙ ) je ona logička operacija koja primenjena na dva iskaza daje iskaz koji je tačan samo ako su oba iskaza u konjukciji tačna, a netačna u svim drugim slučajevima. Iskaze u konjukciji možemo zvati “konjukti”.

Disjunkcija (znak V ) je ona logička operacija koja je netačna samo ako su oba iskaza u disjunkciji netačna, a tačna u svim drugim slučajevima:

Implikacija  (znak → ) je logička operacija koja je netačna samo ako je prvi član implikacije (antecedens) tačan, a drugi član (konsekvens) netačan. Po ovome je implikacija slična svakom valjanom zaključivanju: nesitinit zaključak ne sme slediti iz istinitih premisa.

Ekvivalencija (znak = ) je ona logička operacija koja je tačna samo ako iskazi u ekvivalenciji imaju istu istinitosnu vrednost, odnosno, ako su oba tačni ili oba netačni:

Na ovaj način iskazne operacije su precizno definisane.

U iskaznom računu moguće je definisati 16 binarnih operacija. Definicije ovih 5 osnovnih operatora, kao i druge definicije u logici (a i matematici), stvar su dogovora. Međutim, od ovih dogovora kasnije zavisi sve i oni se moraju poznavati da bi se odredila istinitosna vrednost bilo koje složene formule u iskaznom računu.

Ključne reči: definicije logičkih operacija, tablice istinitosnih vrednosti, unarne operacije, binarne operacije, negacija, konjunkcija, disjunkcija, implikacija, ekvivalencija

Rezime: U lekciji su date definicije osnovnih logičkih operacija, jedne unarne – negacije, i četiri binarne – konjunkcije, disjunkcije, implikacije i ekvivalencije. Istinitosna tabica sa vrednostima složenih iskaza koji nastaju nekom logičkom operacijom su dovoljne i precizne definicije tih operacija.

Vežbanja:

Prevedite sledeće rečenice na jezik iskaznog računa – zamenite proste iskaze implicirane u njima iskaznim promenljivim (p,q,r…) a veznike i, ili, sledi… znakovima za logičke veznike:

Da li ste na odmoru bili u Srbiji ili u inostranstvu?

Ako zagrevamo neki gas, a ne menjamo mu zapreminu, pritisak u njemu raste.

Opadanje vrednosti novca naziva se inflacija.

Šekspir je autor drama “Otelo”, “Hamlet” i “Romeo i Julija”.

Subatomske ćestice mogu imati celi ili polu-celi spin.

Pospremite sobu ili nema plaže!

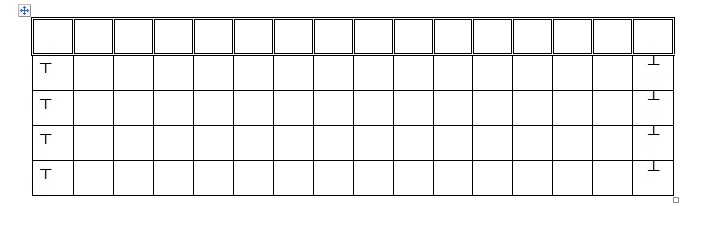
Popunite sledeću tabelu svim varijacijama sa ponavljanjem od elemenata skupa koji ima dva člana (┬ ,┴) dužine 4. Prepoznajte gde se u tabeli nalaze binarne logičke operacije koje smo obradili i upišite njihov znak u polje iznad kombinacije.

Antrfile:

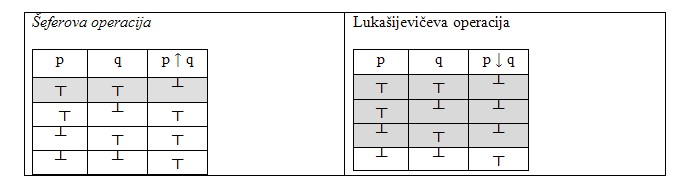
Šeferova i Lukašijevičeva operacija

Pošto su binarne logičke operacije definisane svojim istinitosnim tablicama, moguće je da postoji 16 logičkih operacija koliko ima mogućih varijacija T i ┴ dužine 4. Dve od ovih mogućnosti su logičarima bile posebno interesantne: Šeferova operacija (znak ↑) je u stvari negacija konjunkcije, dok je Lukašijevičeva operacija (znak ↓) negacija disjunkcije. Njihove tablice su dakle:

Zanimljivo je da se pomoću ovih operacija mogu definisati sve ostale operacije u iskaznom računu, na primer pomoću Lukašijevičeve operacije.

┐p = p ↓ p
p v q = (p ↓ q) ↓ (p ↓ q)
p • q = (p ↓ p) ↓ (q ↓ q)

Antrfile

Znaci za logičke operacije

U knjigama iz logike mogu se naći i drugačiji znaci od kod nas uobičajenih , , , , .

Za negaciju se koristi i znak ~,

za konjunkciju znak • ili znak & ili se ona podarzumeva pa je pq isto što i p•q ,

za diskjunkciju je uobičajeno V,

ili   →   se koriste za implikaciju se,

za ekvivalenciju = ili ↔.

Svi ovi zapisi su, naravno, dobri, ako se koriste dosledno.