
Rekli smo već da prema broju premisa i načinu zaključivanja, sva zaključivanja možemo podeliti na neposredna i posredna. Neposredno zaključivanje smo obradili u prethodnoj lekciji. Posredno zaključivanje je zaključivanje koje polazi od dve ili više premisa i kod koga se neki pojmovi koji se pojavljuju u premisama ne pojavljuju u zaključku. Ovi pojmovi nazivaju se „srednji pojmovi“ i služe kao veza preko koje zaključujemo.
Zaključivanje iz samo dve premise naziva se silogizam i predstavlja osnovni oblik posrednog zaključivanja u klasičnoj logici. Silogizme koji kao premise i zaključke imaju jedan od AEIO iskaza, dakle, iskaze u predikatskoj uređenoj formi, detaljno je opisao Aristotel. Na primer, sledeće zaključivanje je silogizam:
Sve velike mačke su mesožderi.
Svi lavovi su velike mačke → Svi lavovi su mesožderi.
U ovom silogizmu:
Sve velike mačke(M) su mesožderi (P).
Svi lavovi (S)su velike mačke (M) → Svi lavovi (S) su mesožderi (P).
pojam „velike mačke“ igra ulogu srednjeg pojma (koji se obično označava slovom M). On se pojavljuje u obema premisama, a nema ga u zaključku. Osim uloge srednjeg pojma tu su još dve uloge pojmova u silogizmu: P, ili veliki pojam, je pojam koji je predikat u zaključku i u uređenom silogizmu se pojavljuje u prvoj, velikoj, premisi, dok je S, mali pojam, pojam koji je subjekat u zaključku i u uređenom silogizmu se pojavljuje u drugoj, maloj, premisi.
Naš silogizam o lavovima je jedan ispravan (valjan), silogizam jer zaključak zaista sledi iz premisa. Ako bismo slučajno ređali AEIO stavove koji sadrže veliki, mali i srednji pojam ponekad bi tako poređani stavovi (najpre dve premise, a za njima zaključak, na primer: AA→E) bili ispravni, a ponekad ne bi (sve mogućnosti za kombinovanje navedeni su u vežbanju u okviru ove lekcije). Da bismo ispravne načine ili oblike zaključivanja odvojili od neispravnih (nevaljanih), logičari su odlučili da isprobaju sve moguće kombinacije premisa i zaključaka i izdvoje ispravne oblike. Prvi je to uradio Aristotel, a mi ćemo sada opisati njegov metod. U stvari, Aristotel je smatrao da su samo tri prve figure silogizma značajne za analizu, a da četvrta figura ne donosi ništa novo. Kasnije je Aristotelova šema figura ipak dopunjena i IV figurom. Mi ćemo se baviti ovom dopunjenom verzijom.
Dakle, u dopunjenoj verziji analize zaključivanja u silogizmu, najpre izdvajamo sve moguće kombinacije položaja termina u iskazu i te kombinacije nazivamo figurama silogizma.
On je najpre izdvojio moguće kombinacije položaja termina u iskazu i te kombinacije je nazvao figurama silogizma. Pošto je definicijama malog, velikog i srednjeg termina, već uveliko određen njihov položaj u premisama i zaključku, ostalo je samo da se varira redosled termina u premisama. Mogućih kombinacija je bilo četiri, pa zato ima četiri figure silogizma, koje se zovu jednostavno I figura, II figura itd. Evo ih:
|
I figura |
II figura |
III figura |
IV figura |
|
M – P S – M → S – P |
P – M S – M → S – P |
M – P M – S → S – P |
P – M M – S → S – P |
Naš gornji silogizam o lavovima bio je silogizam I figure, a stavovi u njemu su svi bili oblika univerzalno-afirmativnog iskaza A, odnosno, AA→A. Naravno, ako sada pogledamo kombinacije AEIO iskaza u okviru jedne figure, ispostavlja se da ih ima 64, što ukupno čini 256 kombinacija ili modusa silogizma. Srećom, kada su ispitani svi ovi modusi ispostavilo se da je među njima samo 24 ispravno, a da je 5 od tih 24 takvo da tvrdi manje od onoga što se moglo zaključiti iz premisa (Na primer, mogli smo zaključiti na E iskaz, da Nijedan S nije P, ali umesto toga tvrdimo samo da Neki S nisu P (O iskaz)). Kada se oduzme ovih 5, ostalo je 19 ispravnih modusa. Videćemo da se taj broj može smanjiti za još 4, ali najpre da vidimo kako su logičari razdvojili ispravne od neispravnih modusa.
Da bi videli koji su modusi ispravni, logičari su morali da ustanove neka pravila valjanog silogizma, pa su prema njima određivali i valjane moduse. Ova pravila su pak podeljena u grupu aksioma silogizma, odnosno, pravila koja se ne dokazuju, i teoreme silogizma, koje su pravila koja se mogu dokazati kao važeća, ako važe aksiome. Za aksiome ispravnog silogizma uzeto je ovih pet pravila:
- Termin (pojam) koji nije razdeljen u premisama, ne može biti raspodeljen ni u zaključku.
- Srednji pojam mora biti raspodeljen barem u jednoj premisi.
- Obe premise ne mogu biti negativne.
- Ako je jedna premisa negativna, i zaključak je negativan.
- Ako su obe premise afirmativne, zaključak mora biti afirmativan.
Kao što vidimo, aksiome silogizma se oslanjaju na pojam raspodeljenosti i na kvalitet iskaza (afirmativni, negativni) o kojima smo govorili ranije.
Na osnovu ovih aksioma mogu se dokazati ove osnovne teoreme koji važe za sve figure silogizma:
- U zaključku mora biti barem za jedan manje raspodeljenih termina, nego što je bilo u premisama.
- Obe premise ne mogu biti partikularne.
- Ako je jedna premisa partikularna, i zaključak je partikularan.
- Premise se ne mogu ređati u kombinaciji IE.
Dokazi ovih teorema nisu teški. Na primer, u zaključku mora biti barem za jedan manje raspodeljenih termina nego u premisama, jer se u premisama nalazi i srednji termin, koji po aksiomi 2, mora biti raspodeljen barem u jednoj premisi, a ne pojavljuje se u zaključku.
Ako primenimo ova pravila na 256 modusa, ostaje onih pomenutih 24. Kao što smo rekli, od tih 24, 5 je takvo da tvrdi manje nego što se može zaključiti, a još 4 modusa predstavljaju zaključivanje iz dve univerzalne premise na partikularan zaključak, što se po savremenom tumačenju logičkog kvadrata ne može činiti, pa broj ispravnih modusa možemo smanjiti na 15.
U srednjem veku, iz mnemotehničkih razloga, ovi modusi su dobili imena u kojima samoglasnici ukazuju od kojih AEIO stavova je neki modus sačinjen. Na primer, gornji modus u kome su i premise i zaključak A stavovi (AA→A) nazvan je BARBARA.
U I figuri, ostala su kao valjana četiri modusa (nazvani su BARBARA, CELARENT, DARII, FERIO), u drugoj takođe 4 ispravna (CESARE, CAMESTRES, FESTINO i BAROCO) u trećoj takođe 4 (DISAMIS, DATISI, FERISON i BOCARDO) i u četvrtoj još tri (CAMENES, DIMARIS i FRESISON). Slova u ovim imenima i njihova pripadnost nekoj od figura daju preciznu informaciju o kakvom obliku silogizma se radi.
Ključne reči: posredno zaključivanje, silogizam, mali, srednji i veliki pojam, figura silogizma, modus silogizma, pravila valjanog silogizma, aksiome silogizma, BARBARA, CELARENT, DARII, FERIO, CESARE, CAMESTRES, FESTINO, BAROCO, DISAMIS, DATISI, FERISON i BOCARDO, CAMENES, DIMARIS i FRESISON.
Rezime: Najpoznatije posredno zaključivanje je silogizam koji predstavlja zaključivanje iz dve premise. Arsitotel je ovo zaključivanje ispitao i uredio, uočivši da u svakom silogizmu imamo 3 pojma (srednji, mali, veliki pojam) i da sve silogizme prema njihovom obliku možemo podeliti u grupe preko figura i modusa silogizma. Kasniji logičari analizirali su 4 figure i 256 mogućih modusa. Međutim, kombinovanje svih mogućnosti ne daje uvek ispravne zaključke. Da li je neki silogizam ispravan utvrđujemo tako što proverimo da li su u njemu poštovana pravila silogizma. Na ovaj način dolazimo do 15 potpuno ispravnih modusa silogizma, koji su poznati po svojim imenima BARBARA; CELARENT…(potpun spisak vidi u ključnim rečima i glavnom tekstu).
Vežbanje:
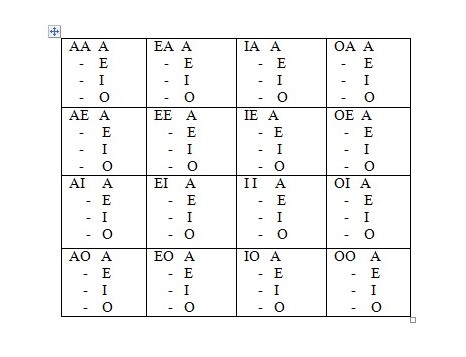
Koristeći pravila silogizma, eliminišite neispravne kombinacije premisa i zaključka iz donje tabele. U tabeli se nalaze 64 moguće kombinacije premisa i zaključaka sastavljene od AEIO iskaza.
Analizirajte sledeće silogizme i odgovorite na pitanje koje pravilo je u njima prekršeno:
1) Neki naučnici su ljubitelji kafe
Neki ljubitelji kafe su doktori nauka.
→ Neki doktori nauka su naučnici
2) Svi stand-up komičari su zabavni.
Svi glumci su zabavni.
→ Svi glumci su stand-up komičari.
3) Svi Italijani su religiozni.
Neke pape nisu Italijani.
→ Neke pape nisu religiozne.
4) Nijedan pevač nije bez sluha.
Nijedan kompozitor nije bez sluha.
→ Svi pevači su kompozitori.
5) Sve autoritarne ličnosti vole vođe.
Neki umetnici ne vole vođe.
→ Nijedan umetnik nije autoritarna ličnost.
Antrfile
Entimem, polisilogizam i sorit
 Entimem je silogizam u kome su jedna premisa ili zaključak prećutani, odnosno podrazumevani, kao kada kažemo „Ne treba se sunčati po jakom suncu, jako sunce može da dovede do opekotina“ (prećutali smo premisu da su opekotine loše) ili „Nijedno živo biće ne treba tući, a ljubimci su živa bića“ (prećutali smo zaključak da ne treba tući ljubimce). Polisilogizam je niz zaključivanja u kojima je zaključak prvog silogizma uzet kao premisa sledećeg itd. Ukoliko to radimo tako da, kao i u entimemu, zaključke ne zapisujemo, već ih samo podrazumevamo dobijamo sorit. Praćenje toka i ispravnosti zaključivanja u ovim obilicima zaključivanja zahteva više pažnje nego što je potrebno za jedan običan silogizam. Pisac Luis Kerol, koji je, kao što smo već rekli, bio i logičar, smislio je jedan zagonetan sorit:
Entimem je silogizam u kome su jedna premisa ili zaključak prećutani, odnosno podrazumevani, kao kada kažemo „Ne treba se sunčati po jakom suncu, jako sunce može da dovede do opekotina“ (prećutali smo premisu da su opekotine loše) ili „Nijedno živo biće ne treba tući, a ljubimci su živa bića“ (prećutali smo zaključak da ne treba tući ljubimce). Polisilogizam je niz zaključivanja u kojima je zaključak prvog silogizma uzet kao premisa sledećeg itd. Ukoliko to radimo tako da, kao i u entimemu, zaključke ne zapisujemo, već ih samo podrazumevamo dobijamo sorit. Praćenje toka i ispravnosti zaključivanja u ovim obilicima zaključivanja zahteva više pažnje nego što je potrebno za jedan običan silogizam. Pisac Luis Kerol, koji je, kao što smo već rekli, bio i logičar, smislio je jedan zagonetan sorit:
Nijedna maca koja voli ribu nije takva da je ne možemo nešto naučiti.
Nijedna maca bez repa neće se igrati sa gorilom.
Mace sa brcima uvek vole ribu.
Nijedn amaca nema repa ako ima brkove.
Prema tome, nijedna maca sa zelenim očima neće se igrati sa gorilom.
Proverite da li je zaključak dobro izveden.







A gde je resenje vezbanja ?