U prošloj lekciji, rekli smo da se broj od 256 mogućih kombinacija AEIO iskaza – modusa silogizma – svodi na 15 ispravnih modusa, po 4 u prve tri figure i tri u četvrtoj. U stvari, ukupno je 24 modusa zadovoljilo aksiome silogizma, ali smo broj 24 smanjili za 9 onih koji zaključuju iz dva univerzalna na partikularan stav, zbog savremenog tumačenja odnosa između univerzalnih i partikularnih stavova.
Ovih 15 preostalih modusa raspoređeni su po figurama na ovaj način:
|
I figura |
II figura |
III figura |
IV figura |
|
M – P S – M → S – P |
P – M S – M → S – P |
M – P M – S → S – P |
P – M M – S → S – P |
|
BARBARA CELARENT DARII FERIO |
CESARE CAMESTRES FESTINO BAROCO |
DISAMIS DATISI FERISON BOCARDO |
CAMENES DIMARIS FRESISON |
Imena ovih modusa i njihova pripadnost nekoj od figura, precizno nam govore kako će izgledati sam silogizam. Na primer, modus BAROCO II figure, imaće srednji termin na mestu predikata u premisama.
P – M
S – M
→ S – P
prva premisa će biti A stav, druga O stav i zaključak će biti O stav, kao što su raspoređeni samoglasnici u imenu modusa BAROCO. Dakle:
Svi P su M
Neki S nisu M
→ Neki S nisu P
Među modusima silogizma, najvažniji su modusi prve figure, jer se ostali modusi od 15 preostalih mogu svesti i obično se u klasičnoj logici svode na moduse prve figure. Zato čemo najpre objasniti te moduse.
Prvi modus I figure, BARBARA, sastoji se od tri A stava. Na primer:
Sve velike mačke su mesožderi.
Svi lavovi su velike mačke.
→ Svi lavovi su mesožderi.
Modus BARBARA je jasan slučaj osnovnog pravila silogizma da ono što važi za sve članove neke klase, važi i za članove posebne potklase u okviru te veće klase.
Drugi modus prve figure CELARENT, koristi dakle E i A stav kao premise, a zaključak je E stav. Na primer:
Nijedna velika mačka nije biljojed.
Svi lavovi su velike mačke.
→ Nijedan lav nije biljojed.
Primer za modus DARII može biti ovaj:
Svi lovci imaju dobar vid.
Neki Japanci su lovci.
→ Neki Japanci imaju dobar vid.
A za modus FERIO, ovaj:
Nijedan lovac nije kratkovid.
Neki Japanci su lovci.
→ Neki Japanci nisu kratkovidi.
Aristotel je moduse prve figure smatrao savršenim silogizmima, pa je svođenje modusa drugih figura na moduse prve figure, smatrao dokazom njihove ispravnosti. I mi možemo slediti taj postupak, ne toliko zbog posebnosti prve figure (u stvari su sve ispravne figure jednake), nego zbog toga da pokažemo da se ovih 15 modusa može svesti na manji broj, odnosno da sve njih povezuje ista logika, isti način razmišljanja.
Na primer, lako je videti da modusi FERIO (I figura) i modusi FESTINO; FERISON; FRESISON, zapravo predstavljaju isti stav u kome je variran redosled pojmova, što se ovde može učiniti jer su obe premise sastavljene od E i I stavova, koji imaju potpunu konverziju:
Ova četiri stava potpuno su, dakle, u logičkom smislu, jednaka:
|
FERIO, I figura: M-P S-M → S-P |
FESTINO, II figura: P-M S-M → S-P |
|
Nijedan lovac nije kratkovid. Neki Japanci su lovci. → Neki Japanci nisu kratkovidi.
|
Nijedan kratkovid nije lovac. Neki Japanci su lovci. → Neki Japanci nisu kratkovidi. |
|
FERISON, III figura: M-P M-S → S-P |
FRESISON, IV figura: P-M M-S → S-P |
|
Nijedan lovac nije kratkovid. Neki lovci su Japanci. → Neki Japanci nisu kratkovidi. |
Nijedan kratkovid nije lovac. Neki lovci su Japanci. → Neki Japanci nisu kratkovidi. |
Slično se može pokazati za moduse DATISI i DISAMIS, treće figure, i DIMARIS četvrte figure, koje se mogu svesti na modus DARII prve figure, konverzijom I premise (DATISI) ili konverzijom I premise, zamenom mesta premisa (DIMARIS) ili konverzijom zaključka i I premise i zamenom mesta premisama (DISAMIS).
Na sličan način se modusi CESARE i CAMESTRES, treće figure, i modus CAMENES četvrte figure mogu svesti na CELARENT, jer i E iskazi imaju potpune konverzije.
Preostali modusi BAROCO, druge figure i BOCARDO, treće figure, mogu se obverzijama i konverzijama premisa svesti na modus FERIO.
Svođenje silogizama drugih figura na silogizme prve figure može biti jedan od načina da ustanovimo da li je neki zaključak ispravan, ili da izvedemo ispravan zaključak.
Ključne reči: modusi silogizma, figure silogizma, svođenje silogizma na moduse I figure, BARBARA, CELARENT, DARII, FERIO, CESARE, CAMESTRES, FESTINO, BAROCO, DISAMIS, DATISI, FERISON i BOCARDO, CAMENES, DIMARIS i FRESISON.
Rezime: Ispravnost zaključka možemo proveriti i tako što proverimo da li njegov oblik potpuno odgovara nekom od ispravnih modusa silogizma. Ispravnih modusa ima 15 a podeljeni su u 4 figure: I (BARBARA, CELARENT, DARII, FERIO), II (CESARE, CAMESTRES, FESTINO, BAROCO), III (DISAMIS, DATISI, FERISON i BOCARDO) IV (CAMENES, DIMARIS i FRESISON). Modusi II, III i IV figure mogu se svesti na moduse prve figure.
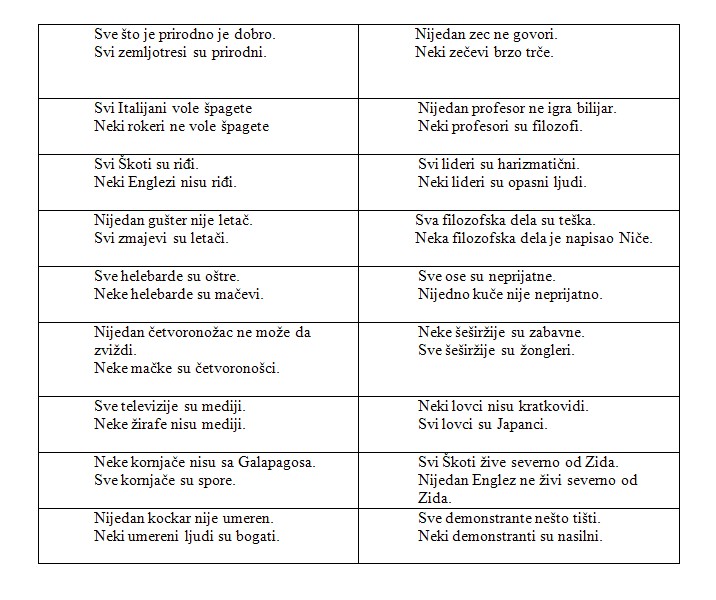
Vežbanje:
Koristeći tabelu ispravnih modusa i posmatrajući primere parova premisa iz donje tabele, odredite:
1. Vrstu stavova u premisama – da li stav ima formu A,E, I ili O,
2. Figuru kojoj pripada silogizam i
3. Ispravam modus silogizma koji se može primeniti u datom slučaju.
Zatim izvedite ispravan zaključak iz datih premisa.
Antrfile:
Modus Ponens i Modus Tolens
Kada smo razmatrali silogizme, bavili smo se isključivo kategoričkim silogizmom, odnosno, silogizmom koji se sastoji samo od kategoričkih iskaza. Međutim, važni su i drugi oblici silogizma, posebno mešoviti hipotetičko-kategorički silogizam, koji se javlja u dva glavna oblika. To su modus ponens (lat. modus ponens) i modus tolens (lat. modus tollens). Primer za modus ponens može biti:
Ako su poleteli pre 1 sat, za koji minut bi trebalo da stignu. (hipotetički stav)
Poleteli su pre 1 sat. (kategorički stav)
Dakle, uskoro stužu.
A za modus tolens:
Ako su krenuli na vreme, već bi trebalo da su tu.
Nema ih.
Dakle, nisu pošli na vreme.
Modus ponens i modus tolens će u okviru iskaznog računa igrati važnu ulogu jer mogu biti uzeti kao osnovne tautologije ili osnovna pravila za gradnju iskaznog računa.