
piše: Vladimir Milutinović
Ovde bih želeo da razjasnimo pitanje šta u stvari znači kada u logici kažemo tvrdnju oblika “Ako…onda…”, na primer, Ako pada kiša, ulice su mokre.
Obično se uzima, da ta tvrdnja u logici znači isto što i u običnom jeziku (životu), odnosno, da tvrdimo uzročnu vezu između padanja kiše i mokrih ulica, ali izgleda da to nije tako.
Da bismo došli do logičkog smisla ove rečenice, najpre bi bilo dobro da se prisetimo jednog od ključnih modernih filozofa – Dejvida Hjuma. On je formulisao tzv. kritiku pojma uzročnosti, koja tvrdi da se nužna veza između dve pojave ne može nikako sasvim potvrditi. Nije moguće navesti logički ili iskustveni argument zbog koga bismo imali pravo da tvrdnju “Iza X će uvek slediti Y” izvedemo iz tvrdnje “ “Do sada je iza X sledilo Y”.
To znači da nikada ne možemo sa punim pravom tvrditi da je X uzrok Y. Pa šta onda možemo tvrditi? Mislim da je odgovor na to pitanje da možemo tvrditi “Moguće je da je X uzrok Y”.
Sada vi možete reći: pa dobro, uvek je moguće da je X uzrok Y, recimo, moguće je da je lepet leptirovih krila u Kini uzrokovao zemljotres na Aljasci. Međutim, to nije sasvim tačno. Moguće je da je X uzrok Y, ali samo ako nemamo očigledan slučaj da se X desilo, a Y nije. U tom slučaju znamo da X nije uzrok Y. U svim ostalim slučajevima možemo samo da tvrdimo da je moguće da je X uzrok Y.
Da se sada vratimo na logiku.
Kada kažemo “Ako p, onda q” ili p → q, onda, po mom mišljenju, kažemo isto što i malopre: “Moguće je da je P dovoljan razlog za q” ili moguće je da je p uzrok q. Mi ne tvrdimo da p jeste dovoljan razlog za q nego da je to moguće.
U našem primeru: “Ako kiša pada, ulice su mokre” – naša tvrdnja ima smisao: “Moguće je da uvek kada kiša pada iz toga sledi da su ulice mokre.”
Da li ova relacija ostaje da važi, ako kiša ne pada? Odnosno, da li ako kiša ne pada (nije tačno da kiša pada), možemo reći da više nije moguće da važi relacija “Ako kiša pada ulice su mokre?”. Pa izgleda da ne. Ako kiša ne pada, bilo da su ulice suve, bilo da su mokre (ulice su očistili čistači), iz toga ne možemo zaključiti da ne važi početna tvrdnja da “Ako kiša pada, ulice su mokre”.
Zbog ovoga istinitosna tablica implikacije ima ovaj oblik:
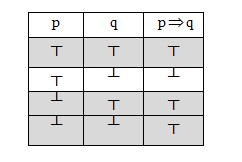
Kada se implikacija interpretira samo ovakvom tablicom, ona se naziva “materijalna implkacija”. Zašto, “materijalna” najčešće se ne objašnjava.
Dakle, ako je prva tvrdnja u implikaciji netačna (kiša ne pada), ne možemo oboriti početnu implikaciju pa ostaje tačno da je moguće da važi uzročna relacija “Ako kiša pada, ulice su mokre”
Logika samo isključuje relacije implikacije koje ne važe, a ne tvrdi da bilo koja sigurno važi.
Kada se tablice koje određuju implikaciju i disjunkciju u logici upotrebe, dobijaju se zanimljive posledice. Naime, formula (p→q)v (q→p) je tautologija, dakle, mora biti istinita. To znači, na primer da jedna od ove dve tvrdnje mora biti istinita:
1) Ako je ovo jaje kuvano, onda će Tramp pobediti na izborima.
2) Ako će Tramp pobediti na izborima, ovo jaje je kuvano.
Međutim, obična intuicija nama govori da bi obe ove tvrdnje mogle biti neistinite, odnosno, da bi kuvano jaje i Trampova pobeda mogli biti uzročno nezavisni događaji, pa se zbog ni iz jednog od njih ne može zaključiti na onaj drugi.
Tu bi trebalo ponovo da se vidi razlika između logike i običnog govora. U običnom govoru, ili u stvarnosti, možemo reći da niko ne bi tvrdio da zna da su jaje i Tramp u uzročnoj vezi, međutim, u logici je stvar drugačija.
Tautologija (p→q)v (q→p) zapravo nam kaže ovo: Ako je slučajno u našem svetu tako da je jaje kuvano a Tramp izgubi na izborima, onda možemo sa sigurnošću da kažemo da prva implikacija ne važi. Međutim, ako ona ne važi, onda je u našem svetu Tramp izgubio na izborima i onda, u našem svetu, ne možemo nikako da oborimo drugu tvrdnju da bi da je on pobedio na izborima jaje bilo kuvano. Uvek ostaje moguće da ona bude istinita, a to je i smisao implikacije u logici.
Tautologije su tvrdnje koje moraju važiti u svim mogućim svetovima. To znači da tvrdnja koja je oboriva u našem svetu sigurno nije tautologija. Takođe, tvrdnja koja je oboriva u bilo kom pojedinačnom mogućem (zamislivom) svetu sigurno nije tautologija (tvrdnja koju bi oborio i naš svet da je drugačiji).
Tautologije nam zapravo kažu koje tvrdnje nisu oborive u bilo kojem pojedinačnom svetu, zato što nam jedan svet može isključiti samo jednu njihovu stranu. Unašem slučaju tautologije (p→q)v (q→p) u jednom svetu moguće je oboriti samo jednu od ove dve implikacije, pa je njihova disjunkcija uvek istinita.
Mi zapravo ne kažemo: “Jedan od dva uzročna smera između bilo koja dva događaja mora postojati”, već
“U jednom svetu može se oboriti samo jedan od dva uzročna smera dok se drugi, upravo ako je prvi oboren, mora ostaviti mogućim”.
Drugim rečima, tautologije su iskazi za koje jedan svet (a uvek nam je dostupan jedan svet, makar i samo zamisliv) nije dovoljan da bi se oni oborili.
Hoću da kažem ovo: kada Kristof Dreser u Logici u svakodnevnom životu (Laguna, 2015) na str. 16 kaže da je njegov profesor tvrdio da je rečenica “Ako je mesec od zelenog sira, onda je broj 5 pijan” tačna, onda je ta tvrdnja zavodljiva u pogrešnom smeru. Profesor svakako nije hteo reći da je ta tvrdnja opisuje naš svet, niti da je ona logički tačna (tautologija), pa je tačna u svakom pa i našem svetu. On je hteo da kaže: “Moguće je da je ova tvrdnja tačna u nekom drugom svetu sa mesecom od zelenog sira i pijanim brojevima, odnosno, u našem svetu svakako ne možemo dokazati da ta tvdnja nije tačna u nekom drugom svetu”. Odnosno, ta tvrdnja nije oboriva u našem svetu, a nije ni tautologija (jer je možda netačna, oboriva, u nekom drugom svetu), pa nije jasan smisao u kome bi uopšte mogla biti nazvana tačnom, osim u ovom našem smislu, da NAŠ svet ostavlja mogućim da ova tvrdnja bude tačna u nekom DRUGOM svetu.
Takođe, kada malo dalje kaže da je “Ako je Berlin glavni grad Nemačke, onda je Angela Merkel savezna kancelarka” istinita rečenica, jer u relaciju implikacije stavlja dva tačna iskaza u našem svetu. Međutim, mislim da bi ispravnije bilo reći, pošto su ovo dve činjenice našeg sveta, moguće je da su one u uzročnoj (logičkoj) vezi, ali to nije izvesno ili istinito. “Implikacija je tačna” u tablici implikacije, znači “moguće je da je tačno ono što tvrdi implikacija”, a ne “tačno je ono što tvrdi implikacija”.
Drugim rečima, bilo koja dva istinita iskaza ne mogu se logički izvesti jedan iz drugoga, niti iz netačnog iskaza sledi logički bilo koj iskaz, niti tačan iskaz sledi iz bilo kog iskaza. U sve delove ove rečenice treba dodati “moguće je”, moguće je da se dva tačna iskaza mogu izvesti jedan iz drugoga, moguće je da iz netačnog iskaza (u našem svetu) u nekom drugom svetu u kome je taj iskaz tačan sledi bilo koji iskaz, moguće je da tačan iskaz, u nekom do svetova, sledi iz bilo kog drugog iskaza.
Ali to ne znači da je u logici istinito da je Angela Merkel kancelarka jer je Berlin glavni grad. U logici je istinito, da ako važi “Ako je Berlin glavni grad, Angela Merkel je kancelarka” i “Berlin je glavni grad Nemačke” onda je tačno“Angela Merkel je kancelarka”. Logika tvrdi da je ovo zaključivanje, zahvaljujući svojoj formi, valjano u svim svetovima, a ne da je bilo koja od premisa tačna u našem svetu.
Logika, u stvari, ne tvrdi ništao bilo kojoj uzročnoj relaciji. Ona ne opisuje naš svet, niti bilo koji svet. Ona nam više govori koje mogućnosti moramo ostaviti otvorenim, ako imamo samo jedan svet pri ruci.
Ako je ova interpretacije relacije implikacije dobra, onda nestaje takozvani “paradoks materijalne implikacije”, odnosno, moguće čuđenje zašto svaka dva istinita iskaza impliciraju jedan drugi (čak i kada nisu povezani na bilo koji način, kaoo jaje i Tramp) ili zašto iz netačnog iskaza sledi bilo koji iskaz.
U našoj interpretaciji, to je zato što implikacija tvrdi da je moguće da dve stvari impliciraju (u značenju, “uzrokuju”) jedna drugu, a ne da je to zaista tako. Neistinit iskaz ne govori nam ništa o mogućoj uzročnoj vezi između stanja koje bi opisivao kada bi bio istinit i nekog drugog stanja. Tu sada nema mesta čuđenju. Zaista je moguće da razne stvari uzrokuju jedna drugu (logika svakako nije ta koja bi odlučivala o tome) ili da odsustvo nekog stanja ne govori ništa o posledicama koje bi imalo eventualno prisustvo nekog stanja.
Inače, ove dve tvrdnje da istinita tvrdnja može slediti iz bilo koje tvrdnje, i da neistinita tvrdnja povlači dozvolu da ako bi bila istinita iz nje može slediti bilo šta, zapisuju se u iskaznom računu preko dve aksiome:
p→(q→p) Aksioma implikacije
┐p→(p→q) Aksioma negacije






