Svođenje na normalnu iskaznu formu je metoda pojednostavljivanja složenih iskaza i metoda koja može poslužiti kao način da se utvrdi da li je neka formula tautologija.
Normalna iskazna forma je forma koja sadrži iskazne promenljive (npr, p, q, r,…) ili njihove negacije (¬p, ¬q, …) povezane u konjukcije ili u disjunkcije.
Na primer stav: (p v q v r) ∙ (p v q) je stav koji ima normalnu formu. Svaki složeni iskaz može se prevesti u normalnu iskaznu formu.
Mogu se razlikovati dva oblika normalne forme iskaza:
1) Konjuktivna normalna forma ima obilk α1 ∙ α2 ∙ α3 … gde su α1 itd. iskazne promenljive, njihove negacije ili disjunkcije.
2) Disjunktivna normalna forma ima obilk α1 v α2 v α3 … gde su α1 itd. iskazne promenljive, njihove negacije ili konjukcije.
Svesti neki iskaz na normalnu iskaznu formu znači transformisati iskaz prema osnovnim tautologijama (ekvivalencijama) koje opisuju kako ekvivalencije, implikacije i negirane konjukcije i disjunkcije zameniti formulama u kojima se javljaju samo elementi koji su dozvoljeni u normalnoj iskaznoj formi.
Primer transformacije:
|
p → (q → p) |
prema pravilu (a → b) = (¬a v b) |
|
p → (¬q v p) |
prema istom pravilu |
|
¬p v (¬q v p) |
prema pravilu o asocijativnosti |
|
(¬p v p) v ¬q (normalna iskazna forma) |
zakon isključenja trećeg (¬p v p) |
|
┬ v ¬q |
tablica za disjunkciju |
|
┬ |
|
|
|
|
Dakle, uvek kad u formuli vidimo ekvivalenciju transformišemo je u konjukciju dve implikacije, uvek kada vidimo implikaciju, transformišemo je u disjunkciju, uvek kada vidimo negaciju konjukcije i disjunkcije transformišemo je prema De Morganovim zakonima ¬ (p v q) =¬p ∙¬q ili isto tako i za konjukciju ¬ (p ∙ q) =¬p v ¬q.
Ako metodom svođenja na normalnu formu želimo da dokažemo da je neka formula tautologija, od koristi su sledeće ekvivalencije:
┬∙ p = p ┴∙ p =┴
┬ v p =┬ ┴ v p = p
Drugim rečima, tačan iskaz (tautologija) se može skratiti iz konjukcije, a netačan (kontradikcija) iz disjunkcije. Opet, ako u disjunkciji imamo tačan iskaz i disjunkcija je tačna, a ako u konjukciji imamo netačan iskaz ta konjukcija je netačna.
Još jedan primer:
|
(p v q) ∙¬p → q |
po pravilu o dsitributivnosti sledi… |
|
(p ∙¬ p) v (q ∙¬p) → q |
skratimo kontradikciju (p ∙¬p) iz disjunkcije |
|
(q ∙¬ p) → q |
po pravilu o implikaciji |
|
¬(q ∙¬ p) v q |
De Morganov zakon |
|
¬ q v ¬ ¬ p v q |
pravilo o dvostrukoj negaciji |
|
¬ q v p v q (disj. normalna forma) |
pravilo o asocijativnosti |
|
¬ q v q v p |
zakon isključenja trećeg (¬q v q) |
|
┬ v p |
tablica za disjunkciju |
|
┬ |
|
|
formula je tautologija |
|
primeri za vežbu: Svedi na normalnu formu i dokaži da je formula tautologija:
p = q
p ∙ p = p
(p → q) v (q → p)
p → (p v q)
((p → q) →p) →p
((p → q) ∙ p) → q
((p → q) ∙ ¬q) → ¬p
¬p → (p → q)
(u lekciji je znak za konjukciju ∙, za ekvivalenciju =, a za implikaciju →)
Antrfile
Binarni brojevi
M oderne binarne brojeve otkrio je Gotfrid V. Lajbnic u 17. veku, mada su ih poznavali i u drevnom Egiptu i srednjovekovnoj Kini i Indiji. Ovi brojevi predstavljaju način da se svaki broj zapiše samo pomoću cifara 0 i 1. Logika binarnog zapisa je da se svaki broj može zapisati kao zbir nekih od ovih brojeva: 1, 2, 4, 8, 16, 32, 64… (ovaj niz je u stvari 20, 21, 22, 23,…itd..).
Na primer 73 = 64+8+1. Binarni zapis se formira tako, što posmatrajući niz 64, 32, 16, 8, 4, 2, 1, ako smo iskoristili određeni broj u našem zbiru, stavljamo cifru 1 na to mesto, a ako nismo, cifru 0. Tako je binarni zapis broja 73 – 1000101. Ne treba posebno naglašavati da je ova dosetka omogućila nastanak računara koji računaju samo pomoću nula i jedinica.
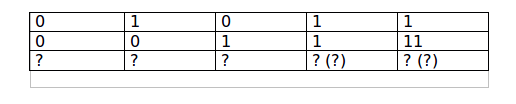
Pravila za sabiranje binarnih brojeva koje koristi računar veoma jednostavna. Pokušajte da ih otkrijete ili da se podsetite kako izgledaju, ako ste se već susreli sa njima. Pomoći će vam pravilo da se, kao i u običnom sabiranju decimalnih brojeva, kreće sa desna na levo, a opcije koje možete imati su date u donjoj tabeli (upitnici u zagradi ukazuju da se nešto „pamti“ za sledeći red sabiranja):