Pošto se sadržaj svakog pojma sastoji od izabranih karakteristika predmeta, svi pojmovi su u neizbežnom odnosu sa drugim pojmovima. Neki od ovih odnosa su češći i značajniji, pa ćemo se ovde pozabaviti njima. Navešćemo 8 osnovnih odnosa među pojmovima:
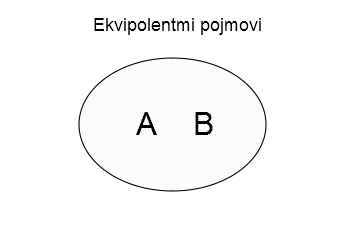
1) Ekvipolentni pojmovi – Ekvipolentni pojmovi su pojmovi koji imaju isti obim, ali različit sadržaj.
Na primer, “Glavni grad Srbije” i “grad na ušću Save i Dunava” su dva (sadržaja) pojma koji se odnose na isti predmet (obim pojma) – grad Beograd. Ovaj odnos iskoristio je jedan od utemeljivača savremene logike Gotlob Frege (1848-1925), da objasni razliku između obima (denotacije) i sadržaja (konotacije) pojma. Njegovi primeri su bili: “Najsjajnija zvezda ujutro – Zvezda Danica” i “Najsjajnija zvezda uveče – Večernjača”. To su dva opisa za isti predmet, planetu Veneru. Iako su obe pojave na nebu bile poznate, dugo se nije znalo da se radi o istoj planeti, pa otuda i dva imena i dva opisa za isto telo. Ovaj odnos pojmova grafički ćemo prikazati ovako (krug je simbol za obim, a slova A i B za različit sadržaj):
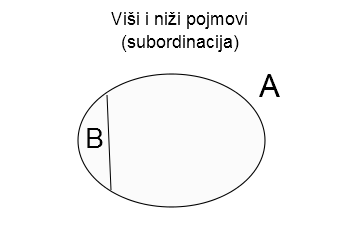
2) Odnos hijerarhije među pojmovima (subordinirani – niži – pojam i superordinirani – viši – pojam) – U ovom odnosu stoje pojmovi od kojih jedan pojam opisujemo kao “viši” ili “širi, opštiji” pojam u odnosu na neki drugi pojam.
Viši pojam ima širi obim, tačnije, obim nižeg pojma je podskup obima višeg pojma. Viši pojam ima i nešto uži sadržaj, pošto je viši pojam potrebno specifikovati (dodati još neku osobinu predmeta) da bismo dobili niži pojam. Na primer, “živo biće” je viši pojam u odnosu na pojam “čovek”, a “paralelogram” viši pojam u odnosu na pojam “romb”, “matematička funkcija” je viši pojam u odnosu na pojam “logaritamska funkcija”. Nauke su prepune pojmova između kojih postoji odnos hijerarhije. U slici:
3) Koordinirani pojmovi – Koordinirani pojmovi su pojmovi koji se nalaze u istoj logičkoj ravni u odnosu na neki viši pojam. Tako su pojmovi “pravougli trougao”, “tupougli trougao” i “oštrougli trougao” koordinirani u odnosu na pojam “trougao”. Pošto su ovo vrste trougla, ako trouglove posmatramo u odnosu na jedan izabrani kriterijum (veličinu uglova), onda koordinirane pojmove možemo opisati i kao pojmove o vrstama nečega.
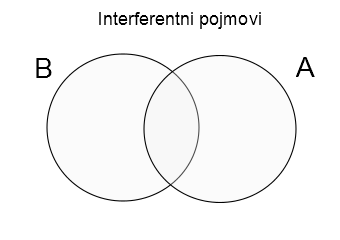
4) Interferentni pojmovi – Interferentni pojmovi su pojmovi čiji obimi imaju presek, odnosno, pojmovi koji se jednim svojim delom obima odnose na isti skup predmeta. Mnogi pojmovi interferiraju, na primer, pojmovi “igrači golfa” i “bivši košarkaši” (u preseku ovih pojmova je svakako Majkl Džordan). Takođe, pojmovi koji potiču iz oblasti kulture često i izrazito interferiraju. Tako su “slova ćirilice” i “slova latinice” interferentni pojmovi. Šema interferencije:
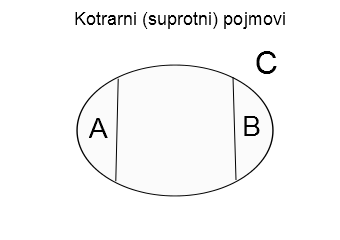
5) Kontrarni (suprotni) pojmovi – Suprotni pojmovi su pojmovi čiji obimi spadaju u obim nekog višeg pojma, ali zauzimaju dva suprotna (udaljena) kraja spektra mogućnosti u okviru obima višeg pojma.
Na primer, “crno” i “belo” su u tom smislu suprotni pojmovi, jer između njih možemo zamisliti mnogo nijansi sive, odnosno, sve druge boje, ako na boje gledamo nanačin uobičajen u svakodnevnom životu (ne i u nauci). Da bi pojmovi bili kontrarni u ovom logičkom smislu, potrebno je da između njih postoji barem jedna, treća mogućnost, odnosno, u našem primeru, ono što nije crno ne mora automatski biti belo, nego postoje i druge mogućnosti. “Pozitivni brojevi” i “negativni brojevi” su suprotni pojmovi ukoliko između njih postoji i broj 0. Ovako opisan pojam suprotnosti možemo nazvati suprotnost u užem smislu, pošto bi suprotnost u širem smislu mogla obuhvatati i protivrečnost, koju ćemo sledeću obraditi.
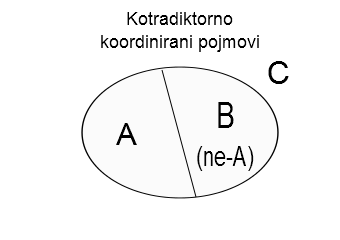
6)Kotradiktorno-koordinirani pojmovi – Kontradiktorno-koordinirani pojmovi nastaju tako što se obim nekog višeg pojma podeli u dve klase u kojima su predmeti koji imaju neku osobinu i, u drugoj klasi, predmeti koji nemaju neku osobinu. Sinonim za “kontradiktorno” je “protivrečno”-
Ako su pojmovi protivrečni, tada ne postoji treća mogućnost – ono što nije A, mora biti B, jer je B isto što i ne-A. I ovakvih pojmova ima puno u svim naukama. Takvi su, na primer: parni i neparni prirodni brojevi, prosti i složeni prirodni brojevi, jednoćelijski i višećelijski organizmi, eukariotske i prokariotske ćelije, kičmenjaci i beskičmenjaci itd. Prednost kontradiktornih pojmova je u tome što oni iscrpljuju obim nekog višeg pojma, pa klasifikacija napravljena na osnovu dva kontradiktorna pojma sigurno obuhvata sve elemente koji potpadaju pod viši pojam (ne može se, recimo, dogoditi da neki realan broj nije ni racionalan ni iracionalan).
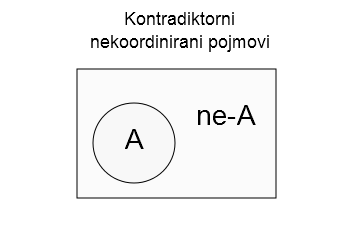
7) Kontradiktorno-nekoordinirani pojmovi – Kotradiktorno-nekoordinirani pojmovi imaju isti odnos kao prethodni par pojmova, s tim da sada nema višeg pojma čiji obim oni dele na dva dela, već se kao viši pojam uzima čitav univerzum (ukupan spektar mogućnosti).
Par pojmova u ovom odnosu možemo napraviti od bilo kog pojma, ako na jednu stranu stavimo skup predmeta na koji se pojam odnosi, a na drugu sve što ne spada u taj skup. Međutim, to nam neće uvek biti korisno. Ipak, u nauci ima dosta ovakvih pojmova, na primer, pojmovi organsko-neorgansko, prirodno-veštačko, pravo-zakrivljeno, konačno-beskonačno su takvi pojmovi. U filozofiji se koriste pojmovi materijalno-nematerijalno koji dele čitav mogući univerzum. Pojmovi prosto-složeno, realno-imaginarno su slični. Okolnost da ovi kontradiktorni pojmovi nemaju viši pojam možemo da grafički prikažemo pravougaonikom koji simbolizuje čitav univerzum, a ne obim nekog određenog višeg pojma.
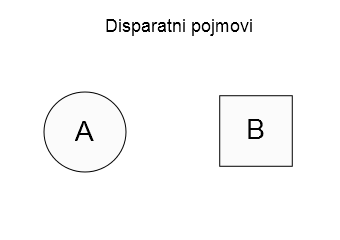
8) Disparatni pojmovi – Disparatni pojmovi su jednostavno pojmovi čiji su sadržaji sastavljeni od pojmova koji su veoma udaljeni po smislu. Takvi su pojmovi “Bog” i “šeširdžija”, koji se javljaju u uzrečici koja naglašava da između nekih predmeta postoji velika razlika. “Kišna glista” i “anksioznost” mogu biti drugi primer.
Pojmovi mogu biti i u mnogim drugim važnim odnosima. Na primer, dosta važno je znati odnos između elementa i sistema u kome se neki element nalazi (na primer, “Periodni sistem elemenata” i “Azot”, ili “Ćelija” i “Jedro”). Važan je i odnos u kome je nešto granični slučaj nečeg drugog, na primer, zakoni njutnovske fizike mogu se posmatrati kao granični slučaj zakona ajnštajnovske fizike (između njih nema značajne razlike ako se tela kreću malim brzinama).
Sadržaj pojmova i odnos između raznih pojmova dolazi posebno do izražaja u naučnim definicijama i klasifikacijama.
Ključne reči: odnosi među pojmovima, ekvipolentni, subordinirani, koordinirani, interferentni, kontrarni (suprotni), kontradiktorni, disparatni pojmovi
Rezime: Pojmovi se mogu naći u različitim odnosima, a u lekciji smo izdvojili najpoznatije i objasnili ekvipolentne, subordinirane, koordinirane, interferentne, kontrarne (suprotne), kontradiktorne i disparatne pojmove. Znati u kom su odnosu pojmovi važno je zbog toga što je odnos sa drugim pojmovima možda najvažniji aspekt sadržaja svakog pojma. Pojmovni aparat svake nauke sadrži pojmove stavljene u odgovarajuće odnose.
Vežbanje:
Kako biste opisali odnos ovih pojmova? Prodiskutujte o mogućim odgovorima.
unutrašnje Spoljašnje
Prosto Složeno
Prirodno Veštačko
Racionalno Iracionalno
Realno Imaginarno
Moguće Nemoguće
Materijalno Nematerijalno
jedno Mnogo
Pravilno Nepravilno
Određeno Neodređeno
Organsko Neorgansko
Ciklično Aciklično
Pokušajte da se setite primera korišćenja ovih pojmova u svakodnevnom životu ili u raznim naukama?
U kom odnosu su sledeći pojmovi:
Levo Desno
Pozitivno Negativno
Toplo Hladno
Veliko Malo
Suvo Mokro
Blizu Daleko
Odredi u kom su odnosu sledeći pojmovi:
Džedaj Bulova algebra
Ptice Sisari
Inke Maje
Film Umetnost
Strip Film
Džez Rok
Bolest Lek
Jovan Jovanović Zmaj (1833-1904), naš poznati pesnik, vaspitač i izdavač, interesovao se i za filozofiju. Poznavao je filozofju Kanta, Hegela, Lajbnica, a sudeći po sledećoj pesmi, Kant mu je bio omiljeni filozof:
I Hegel i Lajbnic, to je meni fantom
Žeđ se moja filozofska gasi samo Kantom.
Sledeća njegova pesma je u stvari o suprotnim (kontrarnim) pojmovima:
Nije sve lepo, što nije ružno
Nije sve veselo, što nije tužno
Gde nema kose nije sve čelo
Nije sve crno, što nije belo
Nije sve zlato, što je žute boje
Nije sve tuđe, što nije moje.
