U uvodnom objašnjenju pojma logike, rekli smo da je logika formalna po svom karakteru, odnosno, da se odnosi samo na najopštija pravila kojih se držimo kada pravilno mislimo. Sada ćemo sa još jedne strane objasniti taj formalni karakter logike.

Naime, možemo reći da su logička pravila u jednom smislu nezavisna od iskustvene ili empirijske istine o našem svetu. Formalnu logiku ne interesuje koji stavovi o svetu su istiniti, već samo to da li stavovi kojima baratamo slede jedni iz drugih ili, možda, protivreče jedni drugima. Postoji i treća mogućnost, da stavovi niti slede jedni iz drugih, niti protivreče jedni drugima, već su logički nezavisni jedni od drugih, kao kad bismo rekli „Kiša ne pada u Kragujevcu“ i „Kiša pada u Kraljevu“. Sve ove odnose detaljno ćemo proučiti baveći se logikom. (Termine „stav“, „tvrdnja“ i „iskaz“ ovde ćemo koristiti sinonimno, kako ne bismo stalno ponavljali istu reč. Stav ili iskaz je svaka rečenica o čijoj se istinitosti možemo pitati. Iz istih razloga sinonimno ćemo koristiti termine „neistina“ i „laž“ iako bi se u nekom drugom kontekstu i među njima mogla napraviti razlika)

U logici zapravo pratimo zaključivanje i procenjujemo da li je ono valjano izvedeno, prema pravilima. Nije nam važno da li su premise ili zaključak sami po sebi istiniti, jer posmatramo samo to da li stavovi slede jedni iz drugih ili ne. Naravno, da nam je dok se bavimo nekom drugom naukom važno da nam i početni stavovi budu istiniti, ali nam dok se bavimo logikom to nije važno jer nju interesuje samo odnos između stavova.

To je osobina logike koja je čini formalnom u odnosu na naš svet. U okviru moderne filozofije 17. Veka, Gotfrid Vilhelm Lajbnic (Gottfried Wilhelm Leibniz, 1646-1716) opisao je tu osobinu logike rečima da logika mora biti istinita u svim mogućim svetovima. Na primer, možemo zamisliti svet u kome ne bi bilo drugih galaksija, u kome bi živi svet izgledao sasvim drugačije itd. U odnosu na takav svet bile bi istinite neke drugačije rečenice od onih koje su istinite u odnosu na naš svet. Međutim, logička pravila bi važila i za razmišljanje o takvom svetu.

Ovu osobinu logike možemo ilustrovati primerom jednog silogizma. Silogizam je zaključivanje iz dve premise određenog tipa. Neka naše premise, odnosno, stavovi od kojih polazimo, budu:
– Svi hobiti su niski.
– Frodo je hobit.
Iz ovih premisa može se izvesti stav „Frodo je nizak“ koji je, prema priči romana „Gospodar prstenova“, tačan. Međutim, ako premise zamenimo drugačijim premisama:
– Svi hobiti su visoki.
– Frodo je hobit.
onda iz njih možemo izvesti stav „Frodo je visok“, koji je netačan prema priči. Oba zaključka su pravilno izvedeni i to na isti način. Pa ipak, jedan je tačan, a drugi netačan. Ono što je nama važno jeste da je zaključivanje iz datih premisa dobro izvedeno, jer nam to garantuje da će zaključak biti istinit pod uslovom da su premise istinite.

U ovoj poslednjoj rečenici krije se i definicija valjanog zaključivanja:

Valjano zaključivanje je ono zaključivanje kod koga zaključak mora biti istinit, ako su premise istinite.

U našem primeru: ako je tačno da su „Svi hobiti niski“ i da je Frodo hobit, onda mora biti tačno i da je Frodo nizak pošto taj zaključak sledi iz ovih premisa. Nije potrebno da to nezavisno proveravamo.

Zaključivanje možemo opisati kao proces u kome iz jednog ili više stavova izvodimo neki novi stav.
Da li je zaključivanje dobro izvedeno uvek treba proveriti. Na primer, iz premisa:
– Sve tune su ribe
– Nijedan losos nije tuna.
ne sledi nijedan zaključak koji bi govorio nešto o ribama i lososima, pa ni onaj koji se po inerciji nameće „Nijedan losos nije riba“.

Da bismo odredili koji zaključak je valjan, možemo koristiti grafičko prikazivanje odnosa pojmova u iskazu u obliku dijagrama. Korišćenje krugova za prikazivanje logičkih odnosa prvi je uveo u logiku švajcarski matematičar Leonard Ojler (LeonhardEuler, 1707-1783) u 18. veku, a dalje je ovu metodu razvio Englez Džon Ven (John Venn, 1834-1923) u 19. veku.
U vežbanju koje sledi nakon ove lekcije pokazaćemo primere ispravnog i neispravnog zaključivanja.

Ključne reči: zaključivanje, valjano zaključivanje, silogizam, premisa, pojam, iskaz, tvrdnja, stav, neistina, laž

Rezime: Logika je formalna i zbog toga što nam u njoj nije prevashodno važno da li su stavovi čije odnose razmatramo istiniti ili nisu, nego samo to da li oni slede jedni iz drugih ili ne. Dakle, važno je samo da li valjano zaključujemo. Valjano zaključivanje definisano je time što valjano zaključivanje obezbeđuje da zaključak sigurno bude istinit, ako su premise od kojih smo pošli istinite, jer taj zaključak logički, prema logičkim pravilima, sledi iz premisa.

Vežbanje:

Ojlerovi dijagrami i valjano zaključivanje

Da bismo ilustrovali kako izgleda analizirano zaključivanje, koristićemo zaključivanje iz dve premise u kome i premise i zaključak moraju biti u jednom od 4 osnovna oblika koje je opisao još Aristotel (384-324 p.n.e.) u svojoj knjizi Organon.

To su ova četiri oblika;

1) Svi S su P (na primer, Svi Škoti su Britanci)
2) Nijedan S nije P (Nijedan Škot nije Britanac)
3) Neki S su P (Neki Škoti su Britanci)
4) Neki S nisu P (Neki Škoti nisu Britanci)

Da bi bilo jasnije koji zaključak sledi iz premisa, svaki oblik iskaza ćemo prikazati pomoću krugova koji će označavati skup na koji se odnose pojmovi koji se pominju u premisama.

1) „Svi Škoti su Britanci“, prikazaćemo kao dva kruga koji su ili jedan u drugom ili se poklapaju. Ukoliko ima Britanaca koji nisu Škoti, kako ćemo ovde pretpostaviti, onda su „Škoti“ predstavljeni manjim krugom u većem krugu koji označava „Britance“:

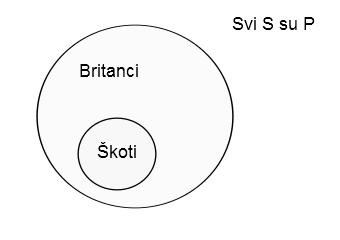
2) „Nijedan Škot nije Britanac“, prikazaćemo kao dva kruga koji se ne seku:
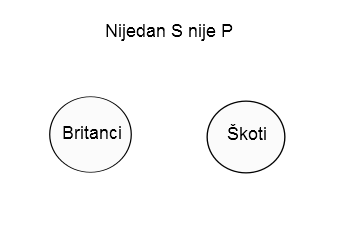3) Tvdnju „Neki Škoti su Britanci“, prikazaćemo kao dva kruga koji se seku. Time smo označili da postoje neki Škoti koji su Britanci (i, samim tim, neki Britanci koji su Škoti), ali ne tvrdimo ništa o tome da li postoje i neki Škoti koji nisu Britanci ili neki Britanci koji nisu Škoti.

(na gornjoj slici je zvezdicom označeno polje, odnosno, skup, u kom sigurno ima elemenata)

4) Rečenicom „Neki Škoti nisu Britanci“, tvrdimo da postoje neki Škoti koji nisu Britanci, ali ne tvrdimo da postoje i neki koji jesu Britanci. Označavamo kao i ranije:

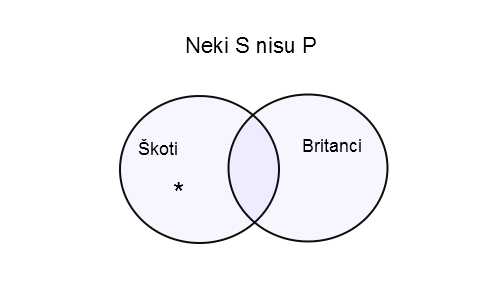
(na gornjoj slici zvezdicom je označeno polje, odnosno, skup, u kom sigurno ima elemenata)

„Neki“ se u logici uvek upotrebljava u značenju „neki, a možda i svi“, odnosno „bar jedan“.

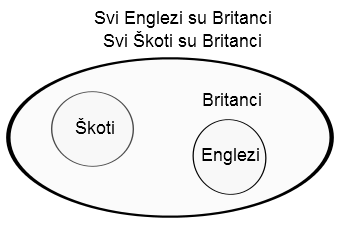
Sada ćemo ove dijagrame iskoristiti za prikaz jednog silogizma. Pošto svaki silogizam u sebi sadrži tri glavna pojma, uvešćemo i pojam „Englezi“. Jedan silogizam mogao bi tada ovako glasiti:

Svi Englezi su Britanci. premise
Nijedan Škot nije Britanac.
? tražimo zaključak

Da bismo došli do zaključka, možemo iskoristiti naše dijagrame. Prvi iskaz je oblika 1) „Svi P su M“, a drugi oblika 2) „Nijedan S nije M“. Ako dijagrame za ove tvrdnje spojimo u jedan dijagram, onda dobijamo:

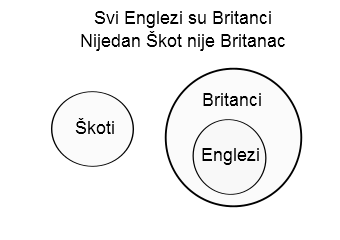
Zaključak se iz slike nameće sam: Nijedan Škot nije Englez, pošto su krugovi koji predstavljaju Škote i Engleze odvojeni (ne seku se).

Da je naš silogizam bio nešto drugačiji, na primer, ovakav:

Svi Englezi su Britanci.
Svi Škoti su Britanci.
?

onda se iz ove dve premise ne bi mogao izvući bilo kakav ispravan zaključak o odnosu Škota i Britanaca. Pošto bi mali krugovi „Škoti“ i „Englezi“ koji su u okviru većeg kruga „Britanaca“ mogli biti u sva četiri moguća odnosa – jedan u drugom (na dva načina), sasvim odvojeni ili sa presekom, a da i dalje ostanu u okviru većeg kruga koji predstavlja Britance – nijedan zaključak se ne može valjano izvući iz premisa.

Odnosi među pojmovima u nekom iskazu mogu se prikazati i pomoću Venovih dijagrama, koji su nešto drugačiji i precizniji od Ojlerovih. Venovi dijagrami koriste uvek istu osnovnu sliku, a dodatnim znacima prikazuju odnose među pojmovima.

Leonard Ojler (Leonhard Euler, 1707-1783) je švajcarski matematičar koji je veći deo svog života proveo u Sankt Petersburgu i Berlinu. Ojler je napisao više od 900 radova u kojima je napravio mnoge pomake u matematici. Prvi je koristio oznake f(x) za funkciju, i za imaginarnu jedinicu, e – za osnovu prirodnog logaritma (današnji Ojlerov broj). Ojler je prvi koristio krugove kako bi prikazao skupove i odnose pojmova u logici. Ojlerov lik nalazi se na jednoj od banknota švajcarskog franka.

Pitanja:

• Obrazloži šta je valjano zaključivanje.
• Kakav je odnos formalne valjanosti zaključivanja i faktičke istinititosti premisa ili zaključka uzetih samih za sebe?
• Šta je silogizam i koji su mogući oblici stavova u uređenom silogizmu? Kako Ojlerovim krugovima možemo prikazati te stavove?