Dokazivanje se može definisati kao proces navođenja argumenata za neku tvrdnju. Kada nešto dokazujemo, navodimo jedan skup iskaza kao opravdanje za prihvatanje tvrdnje čiji nas dokaz interesuje.

Da bismo taj odnos objasnili, poći ćemo od najjednostavnijih primera. Dokaz da smo bili u nekom gradu mogu biti naše fotografije iz tog grada, naš kredibilitet kada tvrdimo da smo tamo bili, iskazi ljudi sa kojima smo bili ili koji su nas tamo videli itd. Dok nas sluša, naš sagovornik na osnovu fotografija, iskaza drugih ljudi i našeg kredibiliteta stiče neki stepen uverenja da smo zaista bili u tom gradu.

Slična dokazivanja neke teze postoje u svim naukama. U matematici se dokazuju teoreme, u fizici ili hemiji hipoteze  o prirodnim zakonima. I u životu ima dokazivanja. Recimo, tužilac u toku nekog suđenja dokazuje da je neko kriv za neko krivično delo. Svi ovi dokazi imaju sličnu osnovnu formu.

Da bismo objasnili kakva je ta osnovna forma, počećemo od toga da svaki dokaz u sebi ima tri bitna dela:

• Tezu (stav koji dokazujemo)
• Argumente (stavove koje navodimo u prilog tezi)
• Logička pravila (pravila koja povezuju argumente i tezu)

Način na koji su teze i argumenti povezani može biti različit. U principu, možemo razlikovati dva osnovna načina povezivanja teze i argumenata – deduktivni i induktivni:

• Prvi, deduktivni, način je onaj u kome teza deduktivno sledi iz argumenata. Odmah ćemo objasniti šta znači “deduktivno”: to znači da, ako su argumenti istiniti, nije moguće da teza bude neistinita. Iz argumenata je moguće valjano (odnosno, deduktivno, što je isto) zaključiti da je teza istinita.
• Drugi, indiktivni, način je takav da se teza ne može deduktivno dokazati na osnovu argumenata (najčešće nekih iskustvenih činjenica). Ipak, tezu prihvatamo baš na osnovu tih argumenata i njihove logičke veze sa našom tezom, ali smo svesni da je u principu moguće da se ispostavi da je teza neistinita, čak iako su nam svi argumenti za nju koje trenutno imamo istiniti.

Prvu varijantu dokaza zvaćemo deduktivni dokaz, a drugu induktivni dokaz. Prvo ćemo opisati induktivni dokaz, zbog toga što je sličniji “dokazima” u svakodnevnom životu.

Induktivni dokaz

Kada ispitujemo osobine neke materije, vršimo konačan broj eksperimenata pod određenim eksperimentalnim uslovima. Ipak, po pravilu, iz toga konačnog skupa rezultata eksperimenata izvodimo zaključke u obliku univerzalnih tvrdnji. Na primer, ako smo zagrevali vodu, uočili smo da voda ključa na 100 ^oC i na osnovu toga zaključili da bismo mogli tvrditi stav: “Tačka ključanja vode je 100 ^oC” ili “Voda uvek ključa na 100 ^oC”. Međutim, ovaj zaključak, iako potpuno u skladu sa metodom empirijske nauke, nije deduktivan, pošto bi se moglo dogoditi da su naše premise dobre (istinite), a da opšti zaključak do koga smo došli nije istinit. To je posledica okolnosti da iz konačnog (partikularnog) skupa argumenata izvodimo tezu koja je mnogo opštija ili univerzalna  (iz istog razloga smo u lekciji o Logičkom kvadratu tvrdili da se iz istinitosti I iskaza ne može izvesti istinitost A iskaza). U stvari, može se dogoditi da voda ne ključa na 100 ^oC, pošto tačka ključanja vode zavisi od atmosferskog pritiska, pa će voda proključati i na manjoj temperaturi, ako je zagrevamo na nekoj planini. Ovakve dokaze koji se pozivaju na eksperimente i na iskustvo nazivamo induktivnim dokazima.

Kada se neka opšta ili univerzalna teza temelji na argumentima koji su dobijeni iz ograničenog skupa iskustava ili na hipotezama koje predstavljaju trenutno najbolja tumačenja i objašnjenja pojava, ona je uvek dokazana samo induktivno i uvek se može dogoditi da bude opovrgnuta.

Ova vrsta dokaza javlja se u svim prirodnim i društvenim naukama, u kojima na osnovu skupa pojedinačnih iskustava zaključujemo na univerzalne zakone. Ponekad, međutim, mnoge prirodne ili društvene nauke sadrže samo pojedinačne činjenice, odnosno, pojedinačne stavove koji izražavaju činjenice ili konglomerate činjenica, pa je mogućnost greške mnogo manja nego kada se teze izražavaju u obliku univerzalnih iskaza.

Deduktivni dokaz

Možemo reći da su induktivni dokaz i iskustvena metoda pravilo u većini nauka. Ipak postoje nauke u kojima su dokazi deduktivni. To su matematika i logika. U tim oblastima znanja argumenti (aksiome) se uzimaju kao visoko verovatni, a sve teze (koje se u ovim naukama zovu “teoreme”) slede deduktivno iz argumenata. U nastavi matematike ste se već susreli sa raznim dokazima matematičkih teorema. Svi ti dokazi su deduktivni dokazi. Oni polaze od opštijih matematičkih iskaza ili aksioma i dokazuju neki novi iskaz koji predstavlja teoremu. Teorema je, ako je dokaz dobro izveden, deduktivno dokazana, što znači da ne može biti neistinita, ako su istiniti stavovi od kojih smo u njenom dokazivanju pošli.

Dakle, matematika i, recimo, fizika su dve fundamentalno različite nauke. U fizici se dokazuje na eksperimentalan, iskustveni način, a u matematici na logički, odnosno, na demonstrativan način. U sledećim lekcijama ćemo se bliže upoznati sa ovom razlikom.

Ključne reči: dokazivanje, dokaz, teza, argument, logička pravila, aksioma, teorema, deduktivni dokaz, induktivni dokaz, demonstrativno dokazati.

Rezime: U lekciji smo naučili koju strukturu ima svaki dokaz (teza, argumenti, logička pravila) i to da u naukama postoje dve vrste dokaza – induktivni i deduktivni. Kod deduktivnog dokaza nije moguće da teza bude neistinita, ako su argumenti istiniti, a kod induktivnog je to ipak moguće.

Vežbanja:

1. Pokušaj da se prisetiš eksperimenata kojima si prisustvovao tokom školovanja.

Da li ih je bilo mnogo? Ako ih nije bilo mnogo, onda je verovatno potrebno da dodatno osvestimo eksperimentalni karakter naučnog saznanja u prirodnim naukama. Prirodne nauke ne mogu da napreduju bez posmatranja i eksperimenata. Mnogi eksperimenti su odigrali prelomnu ulogu u razvoju nauke. Navešćemo neke od njih, a vi proverite da li ste već čuli kako su se oni završili:

• Blez Paskal je poneo barometar (instrument za merenje vazdušnog pritiska) sa sobom kad je krenuo u uspinjanje na jednu planinu. Šta je pokazivao barometar, kako se Paskal penjao?
• Kada se kružna površina obojena u razne boje snažno zavrti, one se izgube, a pojavi se samo jedna boja. Koja?
• Pšenički skrob razmućen u vodi moguće je promešati rukom. Šta će se dogoditi ako pokušate da tu masu udarite rukom?

2. Prouči ove dokaze Pitagorine teoreme. Odredi na šta se ovi dokazi pozivaju (šta su argumenti dokaza):

Dokaz 1.

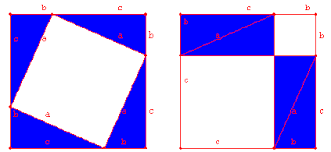
Ovaj dokaz upoređuje dva kvadrata na slici koja su jednaki jer imaju stranicu b+c. U njima su na dva načina ucrtani kvadrati i trouglovi. U prvom načinu, veliki kvadrat u sredini, čija je površina c2 , okružen sa 4 trougla stranica abc. U drugom načinu, dva kvadrata površina a2 i b2 su takođe dopunjeni sa ista ona četiri trougla stranica abc. Pošto kad od istih velikih kvadrata, oduzmemo ista 4 trougla, i ostatak mora biti isti, pa otuda c2 = a2 + b2.

Dokaz 2.

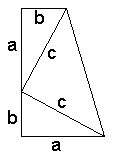
U ovom dokazu površinu trapeza sastavljenog na gornji način, najpre izrazimo na dva načina: 1) kao zbir površina dva trougla i polovine jednog kvadrata, i 2) preko formule za površinu trapeza. Kada sastavimo jedančinu od ovih izraza, sređivanjem te jednačine dobijamo opet c2 = a2 + b2.

Dokaz 3.

Na slici 3. je šema Euklidovog dokaza Pitagorine teoreme. Euklidov dokaz se oslanja najpre na čijenicu da su trouglovi ABF i ACE jednaki (uglovi FAB i CAE su jednaki jer predstavljaju zbir pravog ugla i ugla CAB, stranice FA i AC su jednake kao strane levog gornjeg kvadrata, stranice AB i AE kao strane donjeg kvadrata).

Zatim se konstruiše paralelogram povlačenjem prave iz tačke F koja je paralelna sa duži AB (ovu pravu treba dodati na donju sliku). Ovaj paralelogram se zapravo sastoji od trougla ABF i još jednog identičnog trougla i zato ima površinu duplo veću od trougla ABF.

Zatim se dokazuje da je površina ovog paralelograma jednaka površini kvadrata AFGC, što je pomoćna teorema koju nije teško dokazati.

Po istoj šemi provougaonik AELM jednak je po površini paralelogramu koji nastaje kada se gornja konstrukcija napravi nad trouglom ACE.

Odavde sledi da je površina kvadrata AFGC jednaka površini pravougaonika AELM, odnosno, ako stranicu kvadrata AFGC označimo sa a, ta površina je a2.

Na isti način se može pokazati i da je pravougaonik MLDB jednak b2, ako stranicu kvadrata CHKB označimo sa b.

Pošto ova dva pravougaonika čine donji kvadrat sa površinom c2, tako smo dokazali da je c2 = a2 + b2.